Javascript中的Prim算法
Prim的算法是一种贪婪算法,可为加权无向图找到最小生成树。它找到形成树的边缘子集,该树包括每个顶点,树中所有边缘的总权重最小。
该算法的工作方式是,从任意起始顶点一次构建一个树,在每个步骤中,从树到另一个顶点添加最便宜的连接。
Prim的算法如何工作?
让我们看一下Prim算法的工作原理-
1.选择任意节点作为根节点:在这种情况下,我们选择S节点作为Prim生成树的根节点。该节点是任意选择的,因此任何节点都可以是根节点。有人可能想知道为什么任何视频都可以成为根节点。因此答案是,在生成树中,包括了图的所有节点,并且由于它是连接的,因此必须至少有一条边,它将其连接到树的其余部分。
2.检查出线边缘并选择成本更低的边缘:选择根节点S后,我们看到S,A和S,C是两条权重分别为7和8的边缘。我们选择边S,A,因为它比另一个小。
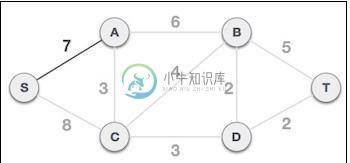
现在,将树S-7-A视为一个节点,我们检查所有从树出的边。我们选择成本最低的一种并将其包括在树中。
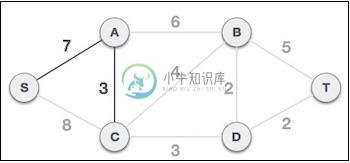
此步骤之后,形成了S-7-A-3-C树。现在,我们再次将其视为节点,并将再次检查所有边缘。但是,我们只会选择成本最低的优势。在这种情况下,C-3-D是新边,比其他边的成本8、6、4等少。
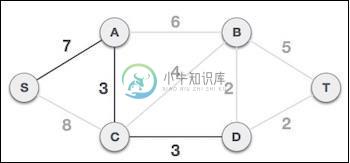
在将节点D添加到生成树之后,我们现在有两个边缘具有相同的代价,即D-2-T和D-2-B。因此,我们可以添加一个。但是下一步将再次使边缘2成本最低。因此,我们显示了一个包含两个边缘的生成树。
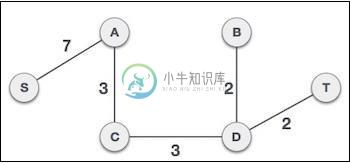
现在让我们看看如何在代码中实现相同的功能-
示例
primsMST() {
//初始化将包含MST的图形
const MST = new Graph();
if (this.nodes.length === 0) {
return MST;
}
//选择第一个节点作为起始节点
let s = this.nodes[0];
//创建一个优先级队列并浏览集
let edgeQueue = new PriorityQueue(this.nodes.length * this.nodes.length);
let explored = new Set();
explored.add(s);
MST.addNode(s);
//将所有从此起始节点开始的边以权重作为优先级添加到PQ-
this.edges[s].forEach(edge => {
edgeQueue.enqueue([s, edge.node], edge.weight);
});
//选取最小的边缘并将其添加到新图形中
let currentMinEdge = edgeQueue.dequeue();
while (!edgeQueue.isEmpty()) {
//继续删除边缘,直到我们得到带有未开发节点的边缘
while (!edgeQueue.isEmpty() && explored.has(currentMinEdge.data[1])) {
currentMinEdge = edgeQueue.dequeue();
}
let nextNode = currentMinEdge.data[1];
//再次检查,因为队列可能会变空而没有退还未开发的元素
if (!explored.has(nextNode)) {
MST.addNode(nextNode);
MST.addEdge(currentMinEdge.data[0], nextNode, currentMinEdge.priority);
//再次将所有边添加到PQ-
this.edges[nextNode].forEach(edge => {
edgeQueue.enqueue([nextNode, edge.node], edge.weight);
});
//将此节点标记为exploredexplored.add(nextNode);
s = nextNode;
}
}
return MST;
}
您可以使用以下方法进行测试:
let g = new Graph();
g.addNode("A");
g.addNode("B");
g.addNode("C");
g.addNode("D");
g.addNode("E");
g.addNode("F");
g.addNode("G");
g.addEdge("A", "C", 100);
g.addEdge("A", "B", 3);
g.addEdge("A", "D", 4);
g.addEdge("C", "D", 3);
g.addEdge("D", "E", 8);
g.addEdge("E", "F", 10);
g.addEdge("B", "G", 9);
g.primsMST().display();
输出结果
这将给出输出-
A->B, D B->A, G D->A, C, E C->D E->D, F G->B F->E
请注意,我们的初始图为-
示例
/** * A * / | \ * C | B * \ | | * D G * | / * E * | * F */
输出结果
我们当前的图看起来像-
/** * A * |\ * C | B * \ | | * D G * | * E * | * F * */
我们删除了最昂贵的边缘,现在有了生成树。
-
一、普里姆算法介绍 普里姆(Prim)算法,是用来求加权连通图的最小生成树的算法。 基本思想 对于图G而言,V是所有顶点的集合;现在,设置两个新的集合U和T,其中U用于存放G的最小生成树中的顶点,T存放G的最小生成树中的边。 从所有uЄU,vЄ(V-U) (V-U表示出去U的所有顶点)的边中选取权值最小的边(u, v),将顶点v加入集合U中,将边(u, v)加入集合T中,如此不断重复,直到U=V为
-
我必须使用基于最小堆的优先级队列来实现Prim的算法。如果我的图包含顶点A、B、C和D以及下面的邻接列表...[它被排序为(顶点名称,相邻顶点的权重)] 粗图: 优先级队列是什么样子的?我不知道该往里面放什么。我应该把所有东西都放进去吗?我应该只写A、B、C和D。我不知道,我真的很想得到答案。
-
亲爱的读者,这些Data Structures & Algorithms Interview Questions专门设计用于让您熟悉在面试Data Structures & Algorithms时可能遇到的问题的本质。 根据我的经验,好的面试官在你的面试中几乎不打算问任何特定的问题,通常问题从这个主题的一些基本概念开始,然后他们继续基于进一步的讨论和你回答的内容: 什么是数据结构? 数据结构是一种
-
Prim用于查找最小成本生成树的算法(如Kruskal算法)使用贪婪方法。 Prim的算法与shortest path first算法共享相似性。 与Kruskal算法相比,Prim的算法将节点视为单个树,并继续从给定图形向生成树添加新节点。 为了与Kruskal的算法形成对比并更好地理解Prim算法,我们将使用相同的例子 - 第1步 - 删除所有循环和平行边缘 从给定图中删除所有循环和平行边。
-
我试图在Java中实现Prim的算法,用于我的图形HashMap LinkedList和一个包含连接顶点和权重的类Edge: 我的想法是,从一个给定的顶点开始:1)将所有顶点保存到一个LinkedList中,这样每次访问它们时我都可以删除它们2)将路径保存到另一个LinkedList中,这样我就可以得到我的最终MST 3)使用PriorityQueue找到最小权重 最后我需要MST,边数和总重量。
-
对于我们最后的图算法,让我们考虑一个在线游戏设计师和网络收音机提供商面临的问题。 问题是他们想有效地将一条信息传递给任何人和每个可能在听的人。 这在游戏中是重要的,使得所有玩家知道每个其他玩家的最新位置。 对于网络收音机是重要的,以便所有该调频的收听者获得他们需要的所有数据来刷新他们正在收听的歌曲。 Figure 9 说明了广播问题。 Figure 9 这个问题有一些强力的解决方案,所以先看看他们

