《金山办公》专题
-
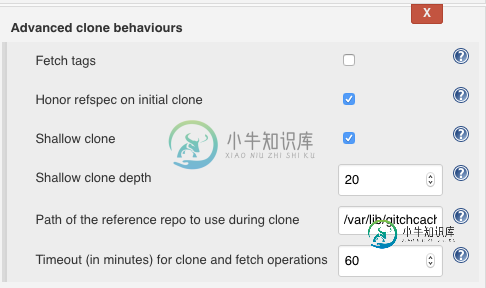 我怎么才能在詹金斯拿到钱?
我怎么才能在詹金斯拿到钱?我正在将SonarQube集成到Jenkins中。我们目前使用浅克隆,因为我们的存储库在历史上完全克隆大型二进制文件的速度很慢。SonarQube需要运行,这显然对浅克隆不起作用。我需要一个解决方案,但我不能更改全局Jenkins配置(它会减慢所有构建)。 情况: 不带参数。 由于没有凭据而获取错误。 我尝试了这个怪物来定制参数,以检出scm: 但我有一个错误: 报告的问题似乎集中在未能提供“存储
-
詹金斯全球管道库目录结构
詹金斯全球管道库项目的正确目录结构是什么?我是groovy的新手,希望确保我从一开始就正确设置了它。。。 这看起来对吗?
-
詹金斯CD管道到库伯内特斯
我打算有一个带有Jenkins的光盘管道,它接受我的应用程序,将码头工人映像发布到我的私人码头工人存储库。我想我知道怎么做。 我不确定的是库伯内特斯部分。我想把那个图像部署到我的私人库伯内特斯集群(目前是1个主集群) 问:安装了 kubectl 和 docker 的詹金斯从站是否需要成为 Kubernetes 集群的一部分才能触发部署?如何触发该部署?
-
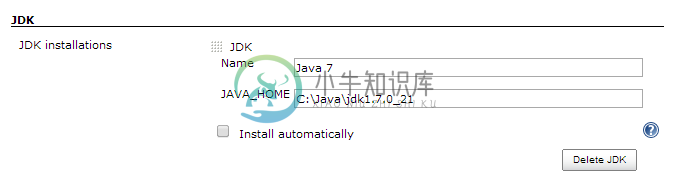 詹金斯不会使用Java 7编译器
詹金斯不会使用Java 7编译器我和一个团队在一个maven项目上工作,我在Jenkins为它建立了一个构建工作。 最近,团队中有人添加了打开字符串的代码。这导致Jenkins中的构建失败,出现以下错误: 所以我当然意识到詹金斯需要使用Java7,而不是Java5。 首先,我远程访问服务器,打开一个cmd,并在java和java版本中执行
-
詹金斯主/从架构的优势?[关闭]
我正在阅读以及如何从这里配置它,当我向下阅读这一页时,我想知道我为什么要这样做,我可以通过它获得什么好处。 我搜索了类似的问题,并到达这里,但仍然不相信相同的。 谁能解释一下我,我可以用同样的方式获得什么好处?
-
关于在GKE设立詹金斯的问题
我在GKE用稳定舵图设置詹金斯(https://github.com/helm/charts/tree/master/stable/jenkins)如中所述https://cloud.google.com/solutions/jenkins-on-kubernetes-engine-tutorial 我是kubernetes/GKE的初学者,想知道如何实现以下目标: 我希望$JENKINS_HOM
-
使用苹果手机录制的金度计
我在用jmeter记录我的https流量时遇到问题,并且总是收到此错误消息。不过,我在记录常规流量方面没有任何麻烦。 响应代码:非HTTP响应代码:javax.net.ssl.SSLHandshakeException响应消息:非HTTP响应消息:java.security.cert.CertificateException:没有可用的X509TrustManager实现 到目前为止,我为克服这个
-
错误运行docker构建詹金斯奴隶
我有一个詹金斯大师,能够从CodeCommit中提取代码。我还设置了一个jenkins slave,这个项目有一个Dockerfile来构建一个图像。当我尝试执行shell命令时, 我得到以下错误:
-
詹金斯:用命令行删除旧版本
我删除旧的jenkins构建与其中的作业托管: 这些旧版本在作业页中仍然可见。如何用命令行删除它们? (在每个构建用户界面中没有删除按钮)
-
回调金字塔甚至与当promise[重复]
我有3个函数我想相继执行,只有当前一个函数完成了它的任务。我用“当promise”库来做这个, 就应该是这样的吗?我的印象是,我可以很容易地避免回调和它的“厄运金字塔”使用promise,还是我使用错了?
-
 兴业数金数据开发面经(已offer)
兴业数金数据开发面经(已offer)两个面试官 一个负责问java一个负责大数据 自我介绍 1.为什么要使用线程池 2.说一下线程池创建时的核心参数 3.如何查看当前线程池最大线程数 4.说一下jvm内存区域 5.说一下有哪些垃圾回收 算法 6.linux通过什么命令查看日志 7.通过什么命令杀死进程 8.说一下spark shuffle 和mr shuffle区别 9.说一下hive有哪几种存储格式 哪种存储格式压缩率更高 10.
-
 兴业数金 数据开发 一面 二面
兴业数金 数据开发 一面 二面#兴业数金一面 ,二面 #数据开发 #23校招 9.23二面(糟心) 全程不看屏幕,全程听不到说啥,全程氛围尬住 1.介绍自己,balabala 2.说说你对数金的了解(他笑了,你知道还挺多) 3.说说你的优势(声音巨小) 4.上个面试咋样 我???那个面试,我,,,那个???? 然后把一面给他复述一遍 5.还记得你的笔试题吗 鬼才记得 6.记得笔试的编程题吗
-
 金蝶软件交互设计【实习】面经
金蝶软件交互设计【实习】面经整个面试过程大约耗时一个小时。因为事先与金蝶用户体验部一名交互设计师(也就是我的面试官)先取好联系,所以当天见面双方都比较放松,氛围很轻松。 首先说明一下,我并不是按照金蝶校招计划进行报名面试的,而是自己私下去联系对方的用户体验部,与对方负责招实习生的hr取得联系,从而获得的面试机会,因此当天只有我一个人面试,所以这份面经仅做参考,但不能代表金蝶交互设计面试的规范流程。 面试刚开始,先是简单自我介
-
 太平金服技术研发面经已o
太平金服技术研发面经已o技术还是研发管培生来着 两轮面试要求正装 一面 技术+主管+hr 主要针对实习、项目、课题深挖 询问遇到的困难,如何解决,详细的功能点,研究方向的介绍和扩展 二面 技术主管+hr 工作地点的考虑 结合研究课题对元宇宙的看法和应用 等等 总体不难 #23届秋招笔面经#
-
傅里叶-莫茨金消元法的应用
傅里叶 - 莫茨金消元法的英文名:Fourier-Motzkin Elimination,简称 FME 算法,它是一种用于从线性不等式中消除变量的数学方法。 它的命名源自于在 1827 年和 1936 年独立发现该算法的 Joseph Fourier 和 Theodore Motzkin 的姓氏。 1. 展示 从线性不等式中消除一组变量,是指通过将关系式中的若干个元素有限次地变换,消去其中的某些元
