《搜索树》专题
-
搜索操作(Search Operation)
搜索过程是Lucene提供的核心功能之一。 下图说明了该过程及其用途。 IndexSearcher是搜索过程的核心组件之一。 我们首先创建包含indexes ,然后将其传递给IndexSearcher ,后者使用IndexReader打开Directory 。 然后我们使用Term创建一个Query ,并通过将Query传递给搜索器来使用IndexSearcher进行搜索。 IndexSearch
-
搜索识别 MIP 页
当你开发完所有的 MIP 网页,并将页面部署到服务器上后,接下来就要考虑页面的流量来源了。本章主要写给站长和搜索引擎维护者,解释 MIP 被搜索引擎识别的两种方法,MIP 搜索引擎的生效过程,以及为了加速 MIP 页面,搜索引擎需要做的 CDN 服务。 MIP 网页可以被独立访问,如直接输入网址或者从被分享的社交网络中打开。 也可以从搜索引擎上进行点击后访问。在这种情况下,为了能够提高速度,百度对
-
插值搜索(Interpolation Search)
插值搜索是二进制搜索的改进变体。 该搜索算法适用于所需值的探测位置。 为使此算法正常工作,数据收集应采用排序形式并均匀分布。 二进制搜索与线性搜索相比具有时间复杂性的巨大优势。 线性搜索具有Ο(n)的最坏情况复杂度,而二分搜索具有Ο(log n)。 存在可以预先知道目标数据的位置的情况。 例如,如果是电话目录,我们是否要搜索Morphius的电话号码。 在这里,线性搜索甚至二进制搜索看起来都很慢,
-
线性搜索(Linear Search)
线性搜索是一种非常简单的搜索算法。 在这种类型的搜索中,逐个对所有项目进行顺序搜索。 检查每个项目,如果找到匹配项,则返回该特定项目,否则搜索将继续,直到数据收集结束。 算法 (Algorithm) Linear Search ( Array A, Value x) Step 1: Set i to 1 Step 2: if i > n then go to step 7 Step 3: if A
-
搜索您的数据
通过在搜索栏输入搜索条件,您可以在匹配当前索引模式的索引中进行搜索。您可以进行简单的文本查询,或使用 Lucene 语法,或使用基于 JSON 的 Elasticsearch 查询 DSL 。 提交一次搜索请求后,直方图、文档列表、字段列表会按新的搜索结果来展示。工具栏上会展示命中的文档数量。文档列表会展示前5条命中的文档。默认情况下,文档列表会按时间倒序进行排列,最新的文档显示在最上面。您可以点
-
7.5 Git 工具 - 搜索
无论仓库里的代码量有多少,你经常需要查找一个函数是在哪里调用或者定义的,或者一个方法的变更历史。 Git 提供了两个有用的工具来快速地从它的数据库中浏览代码和提交。 我们来简单的看一下。 Git Grep Git 提供了一个 grep 命令,你可以很方便地从提交历史或者工作目录中查找一个字符串或者正则表达式。 我们用 Git 本身源代码的查找作为例子。 默认情况下 Git 会查找你工作目录的文件。
-
4.7.分布式搜索
为提高可伸缩性,Sphnix提供了分布式检索能力。分布式检索可以改善查询延迟问题(即缩短查询时间)和提高多服务器、多CPU或多核环境下的吞吐率(即每秒可以完成的查询数)。这对于大量数据(即十亿级的记录数和TB级的文本量)上的搜索应用来说是很关键的。 其关键思想是对数据进行水平分区(HP,Horizontally partition),然后并行处理。 分区不能自动完成,您需要 在不同服务器上设置Sp
-
 快手搜索二面
快手搜索二面直接手撕做sort排序 面试官说其实搜索整个就是一个排序。
-
 微信搜索-一面
微信搜索-一面1、面试官介绍组里干啥的 2、 自我介绍 3、预计实习时间 4、new 和 malloc 区别 5、malloc可以重载吗 6、智能指针 7、**智能指针和裸指针性能区别** 8、智能指针和裸指针访问速度 9、**智能指针内部怎么实现的访问控制** 10、linux排查性能问题 11、linux 排查内存问题 12、介绍一下你的项目 13、epoll如何选择哪个线程处理业务逻辑 14、如何处理惊群
-
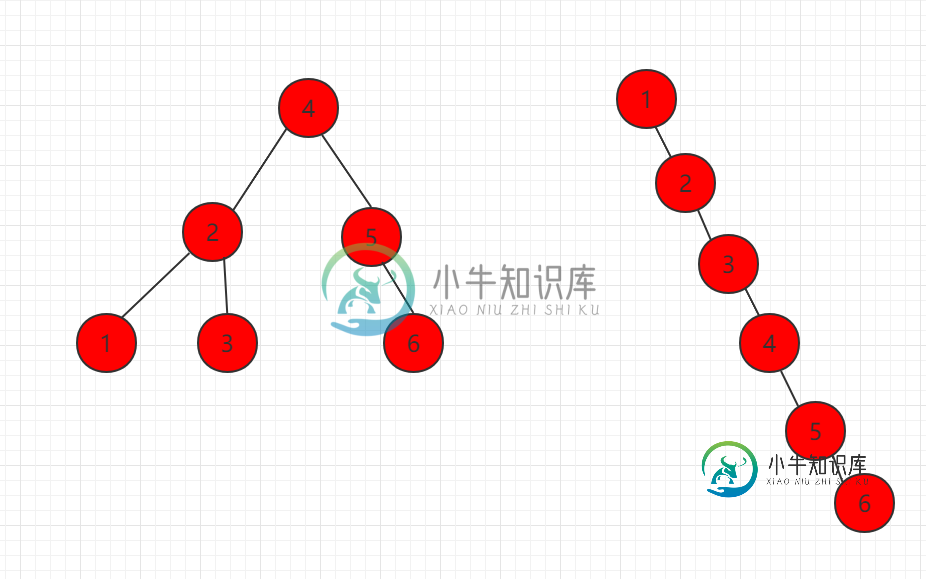 二分搜索树的特性
二分搜索树的特性一、顺序性 二分搜索树可以当做查找表的一种实现。 我们使用二分搜索树的目的是通过查找 key 马上得到 value。minimum、maximum、successor(后继)、predecessor(前驱)、floor(地板)、ceil(天花板、rank(排名第几的元素)、select(排名第n的元素是谁)这些都是二分搜索树顺序性的表现。 二、局限性 二分搜索树在时间性能上是具有局限性的。 如下图
-
删除二进制搜索树
我试着删除二叉查找树的节点,当我打印出来的时候,我得到的结果实际上不是这个删除,实际上可以删除二叉树本身的任何键。 我是二进制搜索树的新手。有人能帮我写代码吗?我们将感谢您的帮助。 谢谢 完整代码
-
修改二进制搜索树
我正在尝试为二叉搜索树类编写一种方法来修改平衡的普通树,这使得树仅在一侧具有节点。 从元素在不平衡树中出现的顺序来看,依序遍历(左、中、右)之间似乎存在某种关系。
-
6.15.平衡二叉搜索树
在上一节中,我们考虑构建一个二叉搜索树。正如我们所学到的,二叉搜索树的性能可以降级到 $$O(n)$$ 的操作,如 get 和 put ,如果树变得不平衡。在本节中,我们将讨论一种特殊类型的二叉搜索树,它自动确保树始终保持平衡。这棵树被称为 AVL树,以其发明人命名:G.M. Adelson-Velskii 和E.M.Landis。 AVL树实现 Map 抽象数据类型就像一个常规的二叉搜索树,唯一
-
C++中的二叉搜索树
我正在学习C++语言,我正在尝试编写BST,但是出了问题。我尝试添加元素到空树,根是NULL,但添加元素后,根仍然是NULL,尽管添加成功了(我在调试模式下看到,节点设置为tmp)。我不知道为什么会这样。
-
验证二进制搜索树
假设BST定义如下: 节点的左子树只包含键小于节点键的节点。节点的右子树只包含键大于节点键的节点。左子树和右子树也必须是二叉搜索树。 示例1:
