《线性表》专题

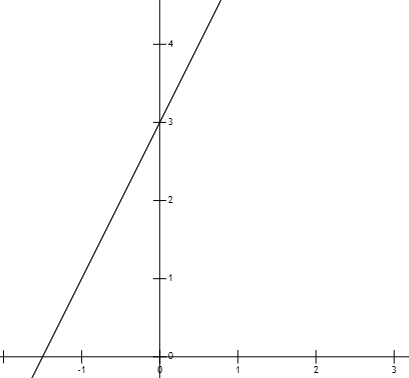
主要内容：一次函数,构建线性模型本节讲解如何构建线性回归算法中的“线性模型”，所谓“线性”其实就是一条“直线”。因此，本节开篇首先普及一下初中的数学知识“一次函数”。 一次函数 一次函数就是最简单的“线性模型”，其直线方程表达式为 ，其中 k 表示 斜率，b 表示 截距，x 为 自变量，y 表示 因变量。下面展示了 y = 2x + 3 的函数图像： 图1：函数图像y=2x+3 函数中斜率 k 与 截距 b 控制着“直线”的“旋

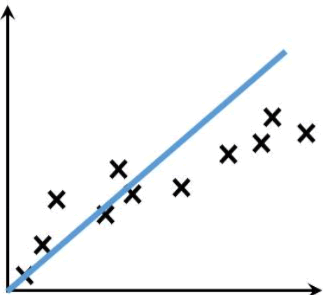
主要内容：线性回归是什么,线性回归方程,实现预测的流程本节我们会认识第一个机器学习算法 —— 线性回归算法（Linear Regression），它是机器学习算法中较为简单，且容易理解的算法模型，你可以把它看做您的第一个“Hello World”程序。 我们先从语义上了解“线性回归”，如果您是第一次接触“线性回归”这个词，那么可以把它分开来看，其中“性代”表线性模型，而“回归”则表示回归问题，也就是用线性模型来解决回归问题。看完上述解释，您脑子中可能

问题内容： 当我阅读“ 实践中的Java并发性 ” c03时，我对以下程序感到困惑： 由于重新排序和线程可见性，循环可能永远不会停止，或者输出可能为零，但是我已经尝试了很多次，并且输出始终为42。所有原因是我太幸运了吗？ 问题答案： 所有的原因是我太幸运了吗？ 不必要。这也将取决于您的处理器体系结构和JVM实现。那就是微妙的内存模型问题的问题之一：它们很难在野外复制。

本文向大家介绍Android LinearLayout 线性布局，包括了Android LinearLayout 线性布局的使用技巧和注意事项，需要的朋友参考一下 示例 LinearLayout是一种ViewGroup将其子级排列在单列或单行中的。可以通过调用方法setOrientation()或使用xml属性来设置方向android:orientation。 垂直方向：android:orien

我对机器学习算法不熟悉，对统计学知识了解不多。我知道这个例子可能不能给你正确的体积预测。然而，让我们考虑我有两个功能和来预测音量。这是样本数据 让我们假设股票是“趋势股票”，在第四天和第五天，股票价值正在上升。我想预测剩余时间框架的音量。在这种情况下，线性回归如何计算数量的产出值？

在我们的应用程序中，我们使用Hystrix，因为我们调用了几个外部服务。我们希望为我们调用的每个外部服务配置一个具有特定大小的线程池。 假设有三个外部服务，称为S1、S2、S3。此外，我们有10个扩展的类，称为C1到C10。 C1和C2调用S1，应该使用相同的线程池，有15个线程。在C1的构造函数内部，我们对进行以下调用： 在一个命令(C1)的构造函数中，我们将S1的线程池大小指定为15。是一个自

我想写一个程序，给定三维空间中的点列表，用浮点表示为x，y，z坐标的数组，在这个空间中输出一条最佳拟合线。直线可以/应该是单位向量和直线上的点的形式。 问题是我不知道这是怎么做的。我发现的最接近的东西是这种联系，尽管老实说，我不明白他是如何从一个方程到另一个方程的，当我们到达矩阵时，我已经迷失了。 有没有一个简单的二维线性回归的泛化，我可以使用/有人可以（数学上）解释上面的链接到方法是否/如何工作

有没有一个简单的pari/gp程序可以筛选k*n c(其中n和c是固定的)形式的数，直到某个素数p，并且k被限制在某个范围内(即k=1，10000，) 伪代码: 换句话说，从整数列表 T 开始 检验素数范围 p 中的第一个素数，并从列表 T 中删除整数 k，使得 k*n c 可以被 p 整除。然后测试下一个素数，依此类推。执行此操作，直到达到筛子返回的极限，或打印候选列表。感谢您的帮助！

我是机器人的新手，我有一些未解决的问题： > 我的项目有两个活动： 欢迎（显示layout1）。 MainDisplay（显示layout2）。

一、什么是线性? 越是基础的概念，越应该有一个透彻的理解，才能对上层问题有直接了当的理解。比如对线性分割器，你对线性有透彻的理解，一看这个名字就大概知道它是怎么回事了。 1. 几何理解：线性关系就是直线关系 现在你可以想象一条曲线S，它可以是直的也可以是弯的，然后你得承认一个事实：曲线S上的任意一点，都可以由曲线S 上其他的任意一点沿着曲线移动而来。 然后我们来看这个移动。在二维坐标平面，移动就意

线性回归小结 线性回归的目的是要得到输出向量Y和输入特征X之间的线性关系，求出线性回归系数θ,也就是 Y=Xθ。其中Y的维度为mx1，X的维度为mxn，而θ的维度为nx1。m代表样本个数，n代表样本特征的维度。 为了得到线性回归系数θ，我们需要定义一个损失函数，一个极小化损失函数的优化方法，以及一个验证算法的方法。损失函数的不同，损失函数的优化方法的不同，验证方法的不同，就形成了不同的线性回归算法

线性回归模型（linear regression） 1.模型定义 给定数据集，$$T={(x{(1)},y{(1)}),(x{(2)},y{(2)}),...,(x{(m)},y{(m)})}$$，其中$$x{(i)}=(1, x_1, x_2, ..., x_n)T\in X= R{n+1}$$，$$y{(i)}\in Y=R$$，线性回归模型试图学到一个通过属性的线性组合来进行预测的函数，即

线性判别分析（Linear Discriminant Analysis，LDA）是一种经典的线性分类方法。它设法将数据集投影到一条直线上，使得同类样例的投影点尽可能接近，异类样例的投影点尽可能远。这样，在分类时，新样本同样投影到这条直线上，根据投影点的位置来确定类别。 由于 LDA 把原来N维的样本投影到了 N-1 维空间，因而也常被视为一种经典的降维技术。 LDA算法 预使得同类样例的投影点尽可

回归分析是一种非常广泛使用的统计工具，用于建立两个变量之间的关系模型。 其中一个变量称为预测变量，其值通过实验收集。 另一个变量称为响应变量，其值来自预测变量。 在线性回归中，这两个变量通过等式相关，其中这两个变量的指数（幂）为1.数学上，线性关系表示绘制为图形时的直线。 任何变量的指数不等于1的非线性关系都会产生一条曲线。 线性回归的一般数学方程是 - y = ax + b 以下是所用参数的说

大多数情况下，我们使用包含多个定量变量的数据集，而分析的目标通常是将这些变量相互关联。 这可以通过回归线来完成。 在构建回归模型时，我们经常检查multicollinearity,我们必须看到连续变量的所有组合之间的相关性，并且如果存在，将采取必要的行动来消除多重共线性。 在这种情况下，以下技术会有所帮助。 绘制线性回归模型的函数 Seaborn中有两个主要功能可视化通过回归确定的线性关系。 这些