《算法引流：》专题

我在网上遇到了这个问题。 给定一个整数：N和一个数组int arr[]，您必须向数组中添加一些元素，以便可以使用（添加）数组中的元素从1生成到N。 请记住，在生成某个x（1）时，只能使用数组中的每个元素一次 有人能给点提示吗？

问题内容： 我需要以任何精度评估任何底数的对数。是否有一种算法？我使用Java编程，所以我对Java代码很好。 问题答案： 使用此身份： log b（n）= log e（n）/ log e（b） 其中可以在任何一个基对数函数，是数量和是基础。例如，在Java中，这将找到以2为底的对数256： 顺便使用base 。还有使用base的。

操作系统实现了各种算法，以便找出链表中的空洞并将它们分配给进程。 关于每种算法的解释如下。 1. 第一拟合算法 第一拟合算法(First Fit)算法扫描链表，每当它找到第一个足够大的孔来存储进程时，它就会停止扫描并将进程加载到该进程中。 该过程产生两个分区。 其中，一个分区将是一个空洞，而另一个分区将存储该进程。 First Fit算法按照起始索引的递增顺序维护链表。这是所有算法中最简单的实现方

主要内容：src/runoob/graph/Path.java 文件代码：图的寻路算法也可以通过深度优先遍历 dfs 实现，寻找图 graph 从起始 s 点到其他点的路径，在上一小节的实现类中添加全局变量 from数组记录路径，from[i] 表示查找的路径上i的上一个节点。 首先构造函数初始化寻路算法的初始条件，from = new int[G.V()] 和 from = new int[G.V()]，并在循环中设置默认值，visited 数组全部为false，fr

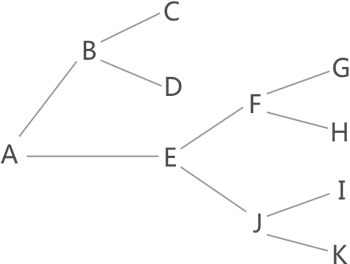
主要内容：回溯算法的应用场景在图 1 中找到从 A 到 K 的行走路线，一些读者会想到用穷举算法（简称穷举法），即简单粗暴地将从 A 出发的所有路线罗列出来，然后逐一筛选，最终找到正确的路线。 图 1 找从A到K的行走路线 图 1 中，从 A 出发的路线有以下几条： A-B-C A-B-D A-E-F-G A-E-F-H A-E-J-I A-E-J-K 穷举法会一一筛选这些路线，最终找到 A-E-J-K 。 本节要讲的回溯算

主要内容：贪心算法的实际应用《 算法是什么》一节讲到，算法规定了解决问题的具体步骤，即先做什么、再做什么、最后做什么。贪心算法是所有算法中最简单，最易实现的算法，该算法之所以“贪心”，是因为算法中的每一步都追求最优的解决方案。 举个例子，假设有 1、2、5、10 这 4 种面值的纸币，要求在不限制各种纸币使用数量的情况下，用尽可能少的纸币拼凑出的总面值为 18。贪心算法的解决方案如下： 率先选择一张面值为 10 的纸币，可以

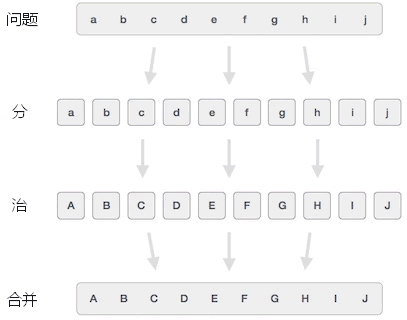
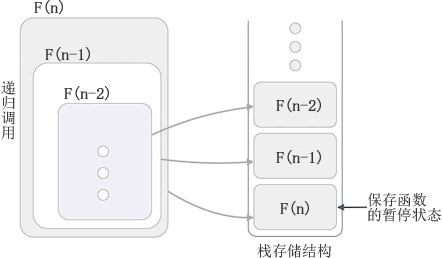
主要内容：分治算法的利弊,分治算法的应用场景实际场景中，我们之所以觉得有些问题很难解决，主要原因是该问题涉及到大量的数据，如果只需要处理少量的数据，问题会变得非常容易解决。 举一个简单的例子，设计一个排序算法实现对 1000 个整数进行排序。对于很多刚刚接触算法的初学者来说，直接实现对 1000 个整数进行排序是非常困难的。而同样的问题，如果转换成对 2 个整数进行排序，解决起来就很容易。 分治算法中，“分治”即“分而治之”的意思。分治算法

主要内容：递归的底层实现机制编程语言中，我们习惯将函数（方法）调用自身的过程称为 递归，调用自身的函数称为 递归函数，用递归方式解决问题的算法称为 递归算法。 函数（方法）调用自身的实现方式有 2 种，分别是： 1) 直接调用自身，例如： 2) 间接调用自身，例如： 程序中，function1() 函数内部调用了 function2() 函数，而 function2() 函数内部又调用了 function1() 函数。也就是

主要内容：回溯VS递归,回溯算法的实现过程回溯算法，又称为 “试探法”。解决问题时，每进行一步，都是抱着试试看的态度，如果发现当前选择并不是最好的，或者这么走下去肯定达不到目标，立刻做回退操作重新选择。这种走不通就回退再走的方法就是回溯算法。 例如，在解决列举集合 {1,2,3} 中所有子集的问题中，就可以使用回溯算法。从集合的开头元素开始，对每个元素都有两种选择：取还是舍。当确定了一个元素的取舍之后，再进行下一个元素，直到集合最后一个元

我有一个由非负整数组成的矩阵。例如： “投下炸弹”将目标单元及其所有八个相邻单元的数量减少一个，至少为零。 确定将所有单元减少到零所需的最小炸弹数量的算法是什么？ B选项（由于我不是一个细心的读者） 事实上，这个问题的第一个版本并不是我要寻找的答案。我没有仔细阅读整个任务，还有其他限制，让我们说： 那么简单的问题呢，当行中的序列必须是非递增的： 是可能的输入序列 不可能，因为7- 也许为“更容易”

问题内容： 在《破解编码面试》第四版中，存在这样的问题： 马戏团正在设计一个塔楼套路，由站在一个人的肩膀上的人组成。出于实际和美学的原因，每个人都必须比其下方的人矮一些和矮一些。考虑到马戏团中每个人的身高和体重，编写一种方法来计算此类塔楼中的最大人数。 示例：输入（ht，wt）：（65，100）（70，150）（56，90）（75，190）（60，95）（68，110） 输出：最长的塔长为6，从上

我们将用于确定最短路径的算法称为“Dijkstra算法”。Dijkstra算法是一种迭代算法，它为我们提供从一个特定起始节点到图中所有其他节点的最短路径。这也类似于广度优先搜索的结果。 为了跟踪从开始节点到每个目的地的总成本，我们将使用顶点类中的 dist 实例变量。 dist实例变量将包含从开始到所讨论的顶点的最小权重路径的当前总权重。该算法对图中的每个顶点重复一次;然而，我们在顶点上迭代的顺序

一、弗洛伊德算法介绍 和Dijkstra算法一样，弗洛伊德(Floyd)算法也是一种用于寻找给定的加权图中顶点间最短路径的算法。该算法名称以创始人之一、1978年图灵奖获得者、斯坦福大学计算机科学系教授罗伯特·弗洛伊德命名。 基本思想 ​ 通过Floyd计算图G=(V,E)中各个顶点的最短路径时，需要引入一个矩阵S，矩阵S中的元素a[i][j]表示顶点i(第i个顶点)到顶点j(第j个顶点)的距离。

一、迪杰斯特拉算法介绍 迪杰斯特拉(Dijkstra)算法是典型最短路径算法，用于计算一个节点到其他节点的最短路径。 它的主要特点是以起始点为中心向外层层扩展(广度优先搜索思想)，直到扩展到终点为止。 基本思想 ​ 通过Dijkstra计算图G中的最短路径时，需要指定起点s(即从顶点s开始计算)。 ​ 此外，引进两个集合S和U。S的作用是记录已求出最短路径的顶点(以及相应的最短路径长度)，而U则是

一、普里姆算法介绍 普里姆(Prim)算法，是用来求加权连通图的最小生成树的算法。 基本思想 对于图G而言，V是所有顶点的集合；现在，设置两个新的集合U和T，其中U用于存放G的最小生成树中的顶点，T存放G的最小生成树中的边。 从所有uЄU，vЄ(V-U) (V-U表示出去U的所有顶点)的边中选取权值最小的边(u, v)，将顶点v加入集合U中，将边(u, v)加入集合T中，如此不断重复，直到U=V为