《算法优化》专题

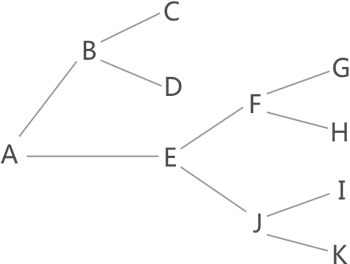
主要内容：回溯算法的应用场景在图 1 中找到从 A 到 K 的行走路线，一些读者会想到用穷举算法（简称穷举法），即简单粗暴地将从 A 出发的所有路线罗列出来，然后逐一筛选，最终找到正确的路线。 图 1 找从A到K的行走路线 图 1 中，从 A 出发的路线有以下几条： A-B-C A-B-D A-E-F-G A-E-F-H A-E-J-I A-E-J-K 穷举法会一一筛选这些路线，最终找到 A-E-J-K 。 本节要讲的回溯算

主要内容：贪心算法的实际应用《 算法是什么》一节讲到，算法规定了解决问题的具体步骤，即先做什么、再做什么、最后做什么。贪心算法是所有算法中最简单，最易实现的算法，该算法之所以“贪心”，是因为算法中的每一步都追求最优的解决方案。 举个例子，假设有 1、2、5、10 这 4 种面值的纸币，要求在不限制各种纸币使用数量的情况下，用尽可能少的纸币拼凑出的总面值为 18。贪心算法的解决方案如下： 率先选择一张面值为 10 的纸币，可以

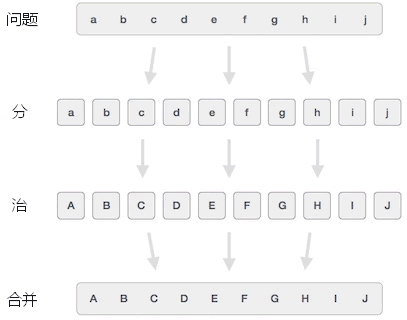
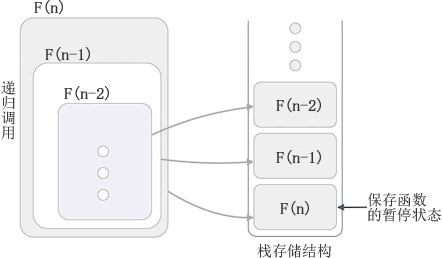
主要内容：分治算法的利弊,分治算法的应用场景实际场景中，我们之所以觉得有些问题很难解决，主要原因是该问题涉及到大量的数据，如果只需要处理少量的数据，问题会变得非常容易解决。 举一个简单的例子，设计一个排序算法实现对 1000 个整数进行排序。对于很多刚刚接触算法的初学者来说，直接实现对 1000 个整数进行排序是非常困难的。而同样的问题，如果转换成对 2 个整数进行排序，解决起来就很容易。 分治算法中，“分治”即“分而治之”的意思。分治算法

主要内容：递归的底层实现机制编程语言中，我们习惯将函数（方法）调用自身的过程称为 递归，调用自身的函数称为 递归函数，用递归方式解决问题的算法称为 递归算法。 函数（方法）调用自身的实现方式有 2 种，分别是： 1) 直接调用自身，例如： 2) 间接调用自身，例如： 程序中，function1() 函数内部调用了 function2() 函数，而 function2() 函数内部又调用了 function1() 函数。也就是

主要内容：回溯VS递归,回溯算法的实现过程回溯算法，又称为 “试探法”。解决问题时，每进行一步，都是抱着试试看的态度，如果发现当前选择并不是最好的，或者这么走下去肯定达不到目标，立刻做回退操作重新选择。这种走不通就回退再走的方法就是回溯算法。 例如，在解决列举集合 {1,2,3} 中所有子集的问题中，就可以使用回溯算法。从集合的开头元素开始，对每个元素都有两种选择：取还是舍。当确定了一个元素的取舍之后，再进行下一个元素，直到集合最后一个元

我有一个由非负整数组成的矩阵。例如： “投下炸弹”将目标单元及其所有八个相邻单元的数量减少一个，至少为零。 确定将所有单元减少到零所需的最小炸弹数量的算法是什么？ B选项（由于我不是一个细心的读者） 事实上，这个问题的第一个版本并不是我要寻找的答案。我没有仔细阅读整个任务，还有其他限制，让我们说： 那么简单的问题呢，当行中的序列必须是非递增的： 是可能的输入序列 不可能，因为7- 也许为“更容易”

问题内容： 在《破解编码面试》第四版中，存在这样的问题： 马戏团正在设计一个塔楼套路，由站在一个人的肩膀上的人组成。出于实际和美学的原因，每个人都必须比其下方的人矮一些和矮一些。考虑到马戏团中每个人的身高和体重，编写一种方法来计算此类塔楼中的最大人数。 示例：输入（ht，wt）：（65，100）（70，150）（56，90）（75，190）（60，95）（68，110） 输出：最长的塔长为6，从上

我们将用于确定最短路径的算法称为“Dijkstra算法”。Dijkstra算法是一种迭代算法，它为我们提供从一个特定起始节点到图中所有其他节点的最短路径。这也类似于广度优先搜索的结果。 为了跟踪从开始节点到每个目的地的总成本，我们将使用顶点类中的 dist 实例变量。 dist实例变量将包含从开始到所讨论的顶点的最小权重路径的当前总权重。该算法对图中的每个顶点重复一次;然而，我们在顶点上迭代的顺序

一、弗洛伊德算法介绍 和Dijkstra算法一样，弗洛伊德(Floyd)算法也是一种用于寻找给定的加权图中顶点间最短路径的算法。该算法名称以创始人之一、1978年图灵奖获得者、斯坦福大学计算机科学系教授罗伯特·弗洛伊德命名。 基本思想 ​ 通过Floyd计算图G=(V,E)中各个顶点的最短路径时，需要引入一个矩阵S，矩阵S中的元素a[i][j]表示顶点i(第i个顶点)到顶点j(第j个顶点)的距离。

一、迪杰斯特拉算法介绍 迪杰斯特拉(Dijkstra)算法是典型最短路径算法，用于计算一个节点到其他节点的最短路径。 它的主要特点是以起始点为中心向外层层扩展(广度优先搜索思想)，直到扩展到终点为止。 基本思想 ​ 通过Dijkstra计算图G中的最短路径时，需要指定起点s(即从顶点s开始计算)。 ​ 此外，引进两个集合S和U。S的作用是记录已求出最短路径的顶点(以及相应的最短路径长度)，而U则是

一、普里姆算法介绍 普里姆(Prim)算法，是用来求加权连通图的最小生成树的算法。 基本思想 对于图G而言，V是所有顶点的集合；现在，设置两个新的集合U和T，其中U用于存放G的最小生成树中的顶点，T存放G的最小生成树中的边。 从所有uЄU，vЄ(V-U) (V-U表示出去U的所有顶点)的边中选取权值最小的边(u, v)，将顶点v加入集合U中，将边(u, v)加入集合T中，如此不断重复，直到U=V为

一、最小生成树 在含有n个顶点的连通图中选择n-1条边，构成一棵极小连通子图，并使该连通子图中n-1条边上权值之和达到最小，则称其为连通网的最小生成树。 例如，对于如上图G4所示的连通网可以有多棵权值总和不相同的生成树。 二、克鲁斯卡尔算法介绍 克鲁斯卡尔(Kruskal)算法，是用来求加权连通图的最小生成树的算法。 基本思想：按照权值从小到大的顺序选择n-1条边，并保证这n-1条边不构成回路。

算法分析 排序 并查集 栈和队列 符号表 其它 参考资料 Sedgewick, Robert, and Kevin Wayne. Algorithms. Addison-Wesley Professional, 2011.

待排序的元素需要实现 Java 的 Comparable 接口，该接口有 compareTo() 方法，可以用它来判断两个元素的大小关系。 使用辅助函数 less() 和 swap() 来进行比较和交换的操作，使得代码的可读性和可移植性更好。 排序算法的成本模型是比较和交换的次数。 // java public abstract class Sort<t extends="" comparable

有三个柱子，分别为 from、buffer、to。需要将 from 上的圆盘全部移动到 to 上，并且要保证小圆盘始终在大圆盘上。 这是一个经典的递归问题，分为三步求解： ① 将 n-1 个圆盘从 from -> buffer ② 将 1 个圆盘从 from -> to ③ 将 n-1 个圆盘从 buffer -> to 如果只有一个圆盘，那么只需要进行一次移动操作。 从上面的讨论可以知道，an