《算法》专题
-
Java计算器核心算法代码实现
本文向大家介绍Java计算器核心算法代码实现,包括了Java计算器核心算法代码实现的使用技巧和注意事项,需要的朋友参考一下 在进行一个表达式的计算时,先将表达式分割成数字和字符串然后利用出入栈将分割后的表达式进行中缀转后缀,再将后缀表达式进行计算得到结果(思想在上一篇写过)现在贴下Java语言的代码实现。(学习Java时间不长所以可能会有很多不足的地方,我会改进也欢迎大神可以给我一些意见和建议~谢
-
Prim算法和Kruskal算法之间的区别
本文向大家介绍Prim算法和Kruskal算法之间的区别,包括了Prim算法和Kruskal算法之间的区别的使用技巧和注意事项,需要的朋友参考一下 在本文中,我们将了解Prim算法和Kruskal算法之间的差异。 最小生成树(MST)的Kruskal算法 给定一个连通图和无向图时,此类图的生成树就是子图,该子图是连接所有顶点的树。 单个图可以具有多个生成树。 加权图,连接图和无向图的最小生成树(M
-
XML签名中的“SignatureMethod”算法与“DigestMethod”算法
我试图通过引用'XML签名语法和处理‘规范来理解这一点。如果有人能证实我的理解是否正确,或者解释这两种算法的作用,我将非常感激。多谢了。
-
如何计算算法的时间复杂度?
我已经通过谷歌和堆栈溢出搜索,但我没有找到一个关于如何计算时间复杂度的清晰而直接的解释。 说代码像下面这样简单: 说一个像下面这样的循环: 这将只执行一次。 时间实际上被计算为而不是声明。
-
通过指针算法计算数组长度
我想知道实际上是如何工作的。我认为这是一种计算数组长度的简单方法,并希望在使用它之前适当地理解它。我对指针算术不是很有经验,但根据我的理解,给出了数组第一个元素的地址。将按地址转到数组的末尾。但是不应该给出这个地址的值吗。而是打印出地址。我真的很感激你帮我把指针的东西弄清楚。 下面是我正在研究的一个简单示例:
-
图的直径计算算法的正确性
null 我相信这个答案是正确的,但我无法证明。有人能证明它为什么起作用或提供一个反例吗?
-
GSP 序列模式分析算法 Gsp 算法
参考资料:http://blog.csdn.net/zone_programming/article/details/42032309 介绍GSP算法是序列模式挖掘算法的一种,他是一种类Apriori的一种,整个过程与Apriori算法比较类似,不过在细节上会略有不同,在下面的描述中,将会有所描述。GSP在原有的频繁模式定义的概念下,增加了3个的概念。 1、加入时间约束min_gap,max_ga
-
 百度3D计算机视觉算法一面
百度3D计算机视觉算法一面9.11 时长正好60min 首先百度是给我最魔幻体验的公司了,因为一开始自己投了另一个也叫计算机视觉的岗,两天就共享中了,结果前几天自己变更了职位给自己捞进来面试了,自己最近疯狂被简历挂收到面试已经属于正反馈了,就冲这一点我这网盘大会员得永久续费了 然后第二点,自己今天的外出任务出了点意外导致不能按原定时间来,本来没报希望问了下HR,结果HR真给我沟通延迟了一小时!呜呜呜度子这恩情你让我怎么还啊
-
 25美团算法笔试0810(算法策略
25美团算法笔试0810(算法策略太疑惑了 超时+不通过 有没有大佬解释一下细节 1. 签到题 判断偶数 2.签到题 根据密码长度数量统计一下即可 3.mex 删除一个耗费x 删除全部k*mex 通过0.85(搞不懂) 4.n个城市大富翁 通过0.5 超时(搞不懂) 5.无线长旗帜 通过0.1 超时
-
算法:使用联合查找来计算岛数
问题内容: 假设您需要计算矩阵上的孤岛数量 当输入矩阵大小适合内存时,我们可以简单地使用DFS或BFS。 但是,如果输入矩阵很大而无法放入内存,该怎么办? 我可以将输入矩阵分块/拆分为不同的小文件,然后分别读取它们。 但是如何合并它们呢? 我陷入了如何合并它们的困境。我的想法是,合并它们时,我们必须阅读一些重叠的部分。但是,这样做的具体方法是什么? 当我在白板上绘制以下示例并逐行处理它时。合并左,
-
 java实现最短路径算法之Dijkstra算法
java实现最短路径算法之Dijkstra算法本文向大家介绍java实现最短路径算法之Dijkstra算法,包括了java实现最短路径算法之Dijkstra算法的使用技巧和注意事项,需要的朋友参考一下 前言 Dijkstra算法是最短路径算法中为人熟知的一种,是单起点全路径算法。该算法被称为是“贪心算法”的成功典范。本文接下来将尝试以最通俗的语言来介绍这个伟大的算法,并赋予java实现代码。 一、知识准备: 1、表示图的数据结构 用于存储图的
-
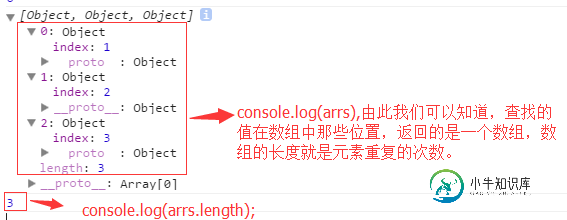 javascript数据结构与算法之检索算法
javascript数据结构与算法之检索算法本文向大家介绍javascript数据结构与算法之检索算法,包括了javascript数据结构与算法之检索算法的使用技巧和注意事项,需要的朋友参考一下 查找数据有2种方式,顺序查找和二分查找。顺序查找适用于元素随机排列的列表。二分查找适用于元素已排序的列表。二分查找效率更高,但是必须是已经排好序的列表元素集合。 一:顺序查找 顺序查找是从列表的第一个元素开始对列表元素逐个进行判断,直到找到了想要的
-
理解Dijkstra算法的时间复杂度计算
每个顶点可以连接到(V-1)个顶点,因此每个顶点的相邻边数是V-1。假设E代表连接到每个顶点的V-1条边。 查找和更新最小堆中每个相邻顶点的权重为O(log(V))+O(1)或 因此,从上面的步骤1和步骤2,更新顶点的所有相邻顶点的时间复杂度是e*(logV)。或. 因此所有V顶点的时间复杂度为V*(E*logv),即。 但Dijkstra算法的时间复杂度为O(ElogV)。为什么?
-
无法计算出此算法的运行时间
我被要求为这个问题编写一个算法:给我们一个数组A,我们想知道数组中是否有两个元素U和L,U和L=K 我是这样写我的算法的: 但问题是,这个算法的运行时间是多少?它是O(nlogn)吗?如果是,为什么?如果不是,我如何在O(nlogn)中实现它?
-
算法计算一个数适合的最小和
给定一组数,找出任意数适合的最小倍数和 < li >集合中的数字可以多次使用(或根本不使用)以获得“总和” < li >这组数字可以是任何正十进制数(即< code>1,4,4.5 ) < li >给定/任意数阈值可以是任意小数(即< code>5 ) > < li> 找出给定数字能与最小余数相适应的倍数组合 找到一个数字可以四舍五入到的最小“总和” 每个组合中使用的实际数字本身对于这个特定的挑战
