如何计算曲线下的部分面积（AUC）

Question

在scikit learn中，您可以使用

roc_auc_score( Y, clf.predict_proba(X)[:,1] )

我只对曲线中假阳性率小于0.1的部分感兴趣。

给定这样一个阈值假阳性率，如何仅计算阈值以上曲线部分的AUC？

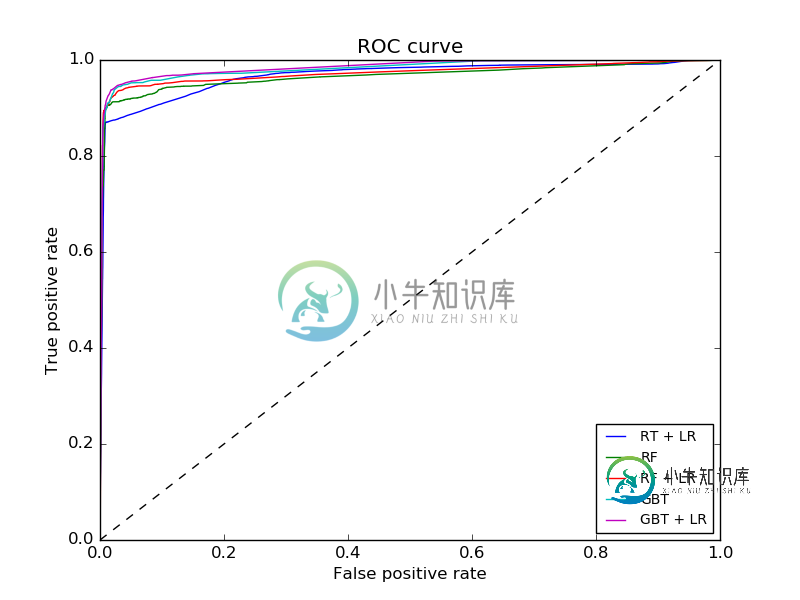
以下是一个具有多条ROC曲线的示例，用于说明：

scikit学习文档展示了如何使用roc_曲线

>>> import numpy as np
>>> from sklearn import metrics
>>> y = np.array([1, 1, 2, 2])
>>> scores = np.array([0.1, 0.4, 0.35, 0.8])
>>> fpr, tpr, thresholds = metrics.roc_curve(y, scores, pos_label=2)
>>> fpr
array([ 0. ,  0.5,  0.5,  1. ])
>>> tpr
array([ 0.5,  0.5,  1. ,  1. ])
>>> thresholds
array([ 0.8 ,  0.4 ,  0.35,  0.1 ]

有没有一种简单的方法可以从这个到部分AUC？

似乎唯一的问题是如何计算fpr=0.1时的tpr值，因为roc_曲线不一定给出该值。

Answer 1

计算您的fpr和tpr值仅在[0.0,0.1]范围内。

然后，您可以使用numpy。trapz评估部分AUC（pAUC），如下所示：

pAUC = numpy.trapz(tpr_array, fpr_array)

此函数使用复合梯形规则来计算曲线下的面积。

Answer 2

Python sklearnroc\u auc\u score（）现在允许您设置max\u fpr。在您的情况下，您可以设置max\u fpr=0.1，该函数将为您计算AUC。https://scikit-learn.org/stable/modules/generated/sklearn.metrics.roc_auc_score.html

Answer 3

让我们从

import numpy as np
from sklearn import  metrics

现在我们设置真实的y和预测的分数：

y = np.array([0, 0, 1, 1])

scores = np.array([0.1, 0.4, 0.35, 0.8])

（请注意，y已将您的问题向下移动了1。这是无关紧要的：无论预测1、2还是0、1，都会获得完全相同的结果（fpr、tpr、阈值等），但有些sklearn。如果不使用0，1，则度量函数是一个阻力。）

让我们看看这里的AUC：

>>> metrics.roc_auc_score(y, scores)
0.75

如您的示例所示：

fpr, tpr, thresholds = metrics.roc_curve(y, scores)
>>> fpr, tpr
(array([ 0. ,  0.5,  0.5,  1. ]), array([ 0.5,  0.5,  1. ,  1. ]))

这给出了以下情节：

plot([0, 0.5], [0.5, 0.5], [0.5, 0.5], [0.5, 1], [0.5, 1], [1, 1]);

通过构造，有限长度y的ROC将由矩形组成：

>

随着阈值持续增加，在离散点，一些负面分类将变为正面分类。

因此，对于有限y，ROC总是由一系列连接的水平线和垂直线组成，从（0，0）到（1，1）。

AUC是这些矩形的总和。这里，如上所示，AUC为0.75，因为矩形的面积为0.5×0.5×0.5×1＝0.75。

在某些情况下，人们选择通过线性插值计算AUC。假设y的长度远大于为FPR和TPR计算的实际点数。然后，在这种情况下，线性插值是介于两者之间的点的近似值。在某些情况下，人们也会猜测，如果y足够大，中间的点会被线性插值<代码>学习。metrics不使用此推测，并获得与sklearn一致的结果。度量，必须使用矩形而不是梯形求和。

让我们编写自己的函数，直接从fpr和tpr计算AUC：

import itertools
import operator

def auc_from_fpr_tpr(fpr, tpr, trapezoid=False):
    inds = [i for (i, (s, e)) in enumerate(zip(fpr[: -1], fpr[1: ])) if s != e] + [len(fpr) - 1]
    fpr, tpr = fpr[inds], tpr[inds]
    area = 0
    ft = zip(fpr, tpr)
    for p0, p1 in zip(ft[: -1], ft[1: ]):
        area += (p1[0] - p0[0]) * ((p1[1] + p0[1]) / 2 if trapezoid else p0[1])
    return area

此函数采用FPR和TPR，以及一个可选参数，说明是否使用梯形求和。运行它，我们得到：

>>> auc_from_fpr_tpr(fpr, tpr), auc_from_fpr_tpr(fpr, tpr, True)
(0.75, 0.875)

我们得到了与sklearn相同的结果。矩形求和的度量，梯形求和的结果不同，更高。

所以，现在我们只需要看看如果我们以0.1的FPR终止，FPR/TPR点会发生什么。我们可以使用对分模块来实现这一点

import bisect

def get_fpr_tpr_for_thresh(fpr, tpr, thresh):
    p = bisect.bisect_left(fpr, thresh)
    fpr = fpr.copy()
    fpr[p] = thresh
    return fpr[: p + 1], tpr[: p + 1]

这是怎么回事？它只是检查fpr中thresh的插入点在哪里。给定FPR的属性（必须从0开始），插入点必须位于水平线上。因此，在此之前的所有矩形应不受影响，在此之后的所有矩形应被删除，而此矩形应可能被缩短。

让我们应用它：

fpr_thresh, tpr_thresh = get_fpr_tpr_for_thresh(fpr, tpr, 0.1)
>>> fpr_thresh, tpr_thresh
(array([ 0. ,  0.1]), array([ 0.5,  0.5]))

最后，我们只需要根据更新版本计算AUC：

>>> auc_from_fpr_tpr(fpr, tpr), auc_from_fpr_tpr(fpr, tpr, True)
0.050000000000000003, 0.050000000000000003)

在这种情况下，矩形和梯形求和得到相同的结果。请注意，一般情况下，它们不会。与sklearn保持一致。指标，应使用第一个指标。