用symphy、python将复方程的指数形式转化为极形式

Question

我正在尝试用python中的Symphy模块求解一个微分方程。这就是我所做的

from sympy import *


t = sympy.Symbol('t')      
k = sympy.Symbol('k')      
m = sympy.Symbol('m')      
x = sympy.Function('x')(t)     

GDE = Eq(m*x.diff(t, 2) + k*x, 0)

solution = dsolve(GDE, x)
display(solution)

现在，我试图得到一个极性形式的解，包括sin，cos和复数项（I），如图所示。在这张图片中，w\n是sqrt（k/m）

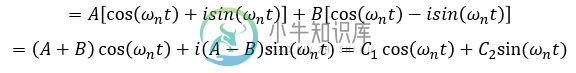
我试过了

solution.rewrite(sin) 

但是它返回一个带有双曲函数的表达式。rewrite（cos）也返回一个带有双曲函数的表达式。

我也试过了

solution.rewrite(sin, cos)

但它给出了最初的答案。

有没有办法把这个指数形式的复形转换成没有双曲函数的极形？

谢谢你

Answer 1

您应该将您的符号声明为实数或正数等。否则默认情况下SymPy假设类似于复数：

In [7]: import sympy

In [8]: from sympy import *
   ...: 
   ...: 
   ...: t = sympy.Symbol('t', real=True)
   ...: k = sympy.Symbol('k', positive=True)
   ...: m = sympy.Symbol('m', positive=True)
   ...: x = sympy.Function('x', real=True)(t)
   ...: 
   ...: GDE = Eq(m*x.diff(t, 2) + k*x, 0)

然后各种简化会自动发生：

In [9]: sqrt(-k/m)
Out[9]: 
ⅈ⋅√k
────
 √m 

In [10]: exp(t * sqrt(-k/m))
Out[10]: 
 ⅈ⋅√k⋅t
 ──────
   √m  
ℯ      

In [11]: exp(t * sqrt(-k/m)).rewrite(cos)
Out[11]: 
     ⎛√k⋅t⎞      ⎛√k⋅t⎞
ⅈ⋅sin⎜────⎟ + cos⎜────⎟
     ⎝ √m ⎠      ⎝ √m ⎠

事实上，根据设定的假设，dsolve将自动给出sin、cos表单：

In [12]: dsolve(GDE)
Out[12]: 
             ⎛√k⋅t⎞         ⎛√k⋅t⎞
x(t) = C₁⋅sin⎜────⎟ + C₂⋅cos⎜────⎟
             ⎝ √m ⎠         ⎝ √m ⎠

如果没有设置这些假设，仍然可以将表达式操作为sin/cos形式，但需要一些force=True来覆盖假设检查：

In [25]: s = solution.rhs; s
Out[25]: 
           _____             _____
          ╱ -k              ╱ -k  
    -t⋅  ╱  ───        t⋅  ╱  ─── 
       ╲╱    m           ╲╱    m  
C₁⋅ℯ             + C₂⋅ℯ           

In [26]: s = expand(s, force=True); s
Out[26]: 
                ___                  ___
               ╱ 1                  ╱ 1 
    -ⅈ⋅√k⋅t⋅  ╱  ─        ⅈ⋅√k⋅t⋅  ╱  ─ 
            ╲╱   m               ╲╱   m 
C₁⋅ℯ                + C₂⋅ℯ              

In [27]: s = s.rewrite(sin); s
Out[27]: 
   ⎛       ⎛         ___⎞      ⎛         ___⎞⎞      ⎛     ⎛         ___⎞      ⎛         ___⎞⎞
   ⎜       ⎜        ╱ 1 ⎟      ⎜        ╱ 1 ⎟⎟      ⎜     ⎜        ╱ 1 ⎟      ⎜        ╱ 1 ⎟⎟
C₁⋅⎜- ⅈ⋅sin⎜√k⋅t⋅  ╱  ─ ⎟ + cos⎜√k⋅t⋅  ╱  ─ ⎟⎟ + C₂⋅⎜ⅈ⋅sin⎜√k⋅t⋅  ╱  ─ ⎟ + cos⎜√k⋅t⋅  ╱  ─ ⎟⎟
   ⎝       ⎝     ╲╱   m ⎠      ⎝     ╲╱   m ⎠⎠      ⎝     ⎝     ╲╱   m ⎠      ⎝     ╲╱   m ⎠⎠

In [28]: s = expand(s).collect(s.atoms(sin, cos)); s
Out[28]: 
             ⎛         ___⎞                     ⎛         ___⎞
             ⎜        ╱ 1 ⎟                     ⎜        ╱ 1 ⎟
(C₁ + C₂)⋅cos⎜√k⋅t⋅  ╱  ─ ⎟ + (-ⅈ⋅C₁ + ⅈ⋅C₂)⋅sin⎜√k⋅t⋅  ╱  ─ ⎟
             ⎝     ╲╱   m ⎠                     ⎝     ╲╱   m ⎠

In [29]: s = powsimp(s, force=True); s
Out[29]: 
             ⎛         ___⎞                     ⎛         ___⎞
             ⎜        ╱ 1 ⎟                     ⎜        ╱ 1 ⎟
(C₁ + C₂)⋅cos⎜√k⋅t⋅  ╱  ─ ⎟ + (-ⅈ⋅C₁ + ⅈ⋅C₂)⋅sin⎜√k⋅t⋅  ╱  ─ ⎟
             ⎝     ╲╱   m ⎠                     ⎝     ╲╱   m ⎠

In [30]: s = powsimp(s, force=True, deep=True); s
Out[30]: 
             ⎛      ___⎞                     ⎛      ___⎞
             ⎜     ╱ k ⎟                     ⎜     ╱ k ⎟
(C₁ + C₂)⋅cos⎜t⋅  ╱  ─ ⎟ + (-ⅈ⋅C₁ + ⅈ⋅C₂)⋅sin⎜t⋅  ╱  ─ ⎟
             ⎝  ╲╱   m ⎠                     ⎝  ╲╱   m ⎠