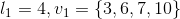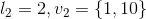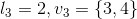修正硬币变化的伪多项式时间算法
我在考虑换硬币时想到了以下问题,但我不知道一个有效的(伪多项式时间)算法来解决它。我想知道是否有任何伪多项式时间的解决方案,或者一些经典的文献,我遗漏了。
硬币变化问题有一个著名的伪多项式时间动态规划解决方案,它问以下问题:
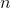
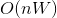
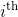
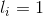
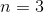
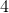
- 取硬币仅此,将此硬币指定为具有值
- 取硬币仅此,将此硬币指定为具有值
- 取硬币和,将其赋值为具有值和,或和,它们分别被认为是相同的方式
- 取硬币,和,并将其赋值为具有值,和
我遇到的问题正是第三种情况;修改这个问题的经典动态编程解决方案很容易,但是它会把这两个子集算作独立的,因为分配了不同的值,即使获得的硬币是相同的。
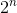
你能给我提供一个伪多项式时间算法来解决这个问题吗,或者它能被证明不存在,除非,比如说,P=NP?也就是说,这个问题是NP完全的(或类似的)。
共有1个答案
也许这很难,但你问问题的方式似乎不是这样。
以硬币1和3为例,分别赋予它们7和3的值,或赋予它们6和4的值,它们被认为是相同的方式。
让我们这样编码两个等价的解决方案:
- ((1,3)、(7,3))
- ((1,3)、(6,4))
现在,当我们记忆一个解时,我们不能问对的第一个元素(1,3)是否已经被解了吗?然后我们将抑制计算(6,4)解。
-
我见过很多硬币更换问题,这个问题很独特。我尝试使用DP和递归,但我无法解决它。 这就是问题所在: 假设给定一个价格,X,其中X是美分,我有5种有限面额的硬币,1,5,10,20,50。我有不同数量的1、5、10、20、50分硬币。我想用最大数量的硬币来确定价格X。我该怎么做?(假设X总是可以用手头的硬币制作) 例如,如果价格X=52,并且 我有三枚一分硬币 我有四枚五分硬币 我有8枚10美分的硬币
-
我们得到了一套面额和总额。 每种面额的无限硬币都可以买到 所有面额都是5的幂 我们必须找到总数所需的最低硬币数量。 我想知道解决方案背后的逻辑。提前感谢。
-
给定一个值N,如果我们想改变为N美分,并且我们有无限量的S={S1,S2,...,Sm}值的硬币,我们有多少种方法可以改变?硬币的顺序并不重要。不过还有一个额外的限制:你只能用正好是K的硬币换零钱。 例如,对于N=4,k=2和S={1,2,3},有两个解:{2,2},{1,3}。所以输出应该是2。 解决方案: 以上是递归解决方案。但是,我需要有关动态规划解决方案的帮助: 让表示与元素和硬币的总和。
-
我理解硬币兑换问题的贪婪算法(用尽可能少的硬币支付特定金额)是如何工作的——它总是选择面额最大但不超过剩余金额的硬币——并且它总是为特定的硬币组找到正确的解决方案。 但对于某些硬币集,贪婪算法会失败。例如,对于集合和总和30,贪婪算法首先选择25,剩下5,然后选择5个1,总共6枚硬币。但是,对于最少数量的硬币,解决方案是选择15枚硬币两次。 一组硬币必须满足什么条件,才能让贪婪算法找到所有总数的最
-
问题:我很难找到达到特定金额所需的最低硬币数量。我很确定这是最简单的递归方式,使用动态编程方法,我基本上应该得到Math.min(“获取ACoin”、“离开ACoin”);不幸的是,我的代码不会终止,尽管我确实有在满足总和的条件下终止的if语句,硬币数组耗尽,或者如果总和结束。请查看下面的代码,让我知道我做错了什么,特别是为什么我的代码继续执行,直到它收到一个stackoverflow错误,尽管我
-
我试图用递归来解决硬币兑换问题,遇到了下面的代码。 问题:给定一些面额的无限硬币,计算它们形成给定数量的方式。 输入: 代码: 我理解代码本身,也理解基本情况,但是我不理解它是如何封装递归/解决方案的。 例如,如果我正在求解,我可以说,因此我可以清楚地“看到”递归。在换硬币的例子中,我无法推断出类似的关系。有人能帮我吗?