六角网格(平顶)距离计算
public void setQR(int theQ, int theR){
this.q = theQ;
this.r = theR;
this.x = this.q;
this.z = this.r - (this.q - (this.q&1)) /2;
this.y = -(this.x + this.z);
}
private double distance = 0;
public double workOutDistance(Hexagon hexagon, HexagonFood target){
double targetX = target.getCPX();
double targetY = target.getCPY();
double hexagonX = hexagon.getCPX();
double hexagonY = hexagon.getCPY();
double deltaX = (targetX-hexagonX)*-1;
double deltaY = (targetY-hexagonY)*-1;
double deltaXRadius = (deltaX/(SimField.hexSize)/1.5);
double deltaYApothem = (deltaY/(SimField.hexSize/1.155)/2);
hexagon.setQR((int)deltaXRadius, (int)deltaYApothem);
ArrayList<Integer> coords = new ArrayList<>();
coords.add(
Math.abs(hexagon.getX() - target.getX())
);
coords.add(
Math.abs(hexagon.getZ() - target.getZ())
);
coords.add(
Math.abs(hexagon.getY() - target.getY())
);
System.out.println(coords);
distance = Collections.max(coords);
return distance;
}
改变这个..
public void setQR(int theQ, int theR){
this.q = theQ;
this.r = theR;
this.x = this.q;
this.z = this.r - (this.q - (this.q&1)) /2;
this.y = -(this.x + this.z);
}
对此..
public void setQR(int theQ, int theR){
this.q = theQ;
this.r = theR;
this.x = this.q;
if (this.r>0){
this.z = this.r - (this.q - (this.q&1))/2;
}
else {
this.z = this.r - (this.q + (this.q&1))/2;
}
this.y = -(this.x + this.z);
}
暂时还没有答案
-
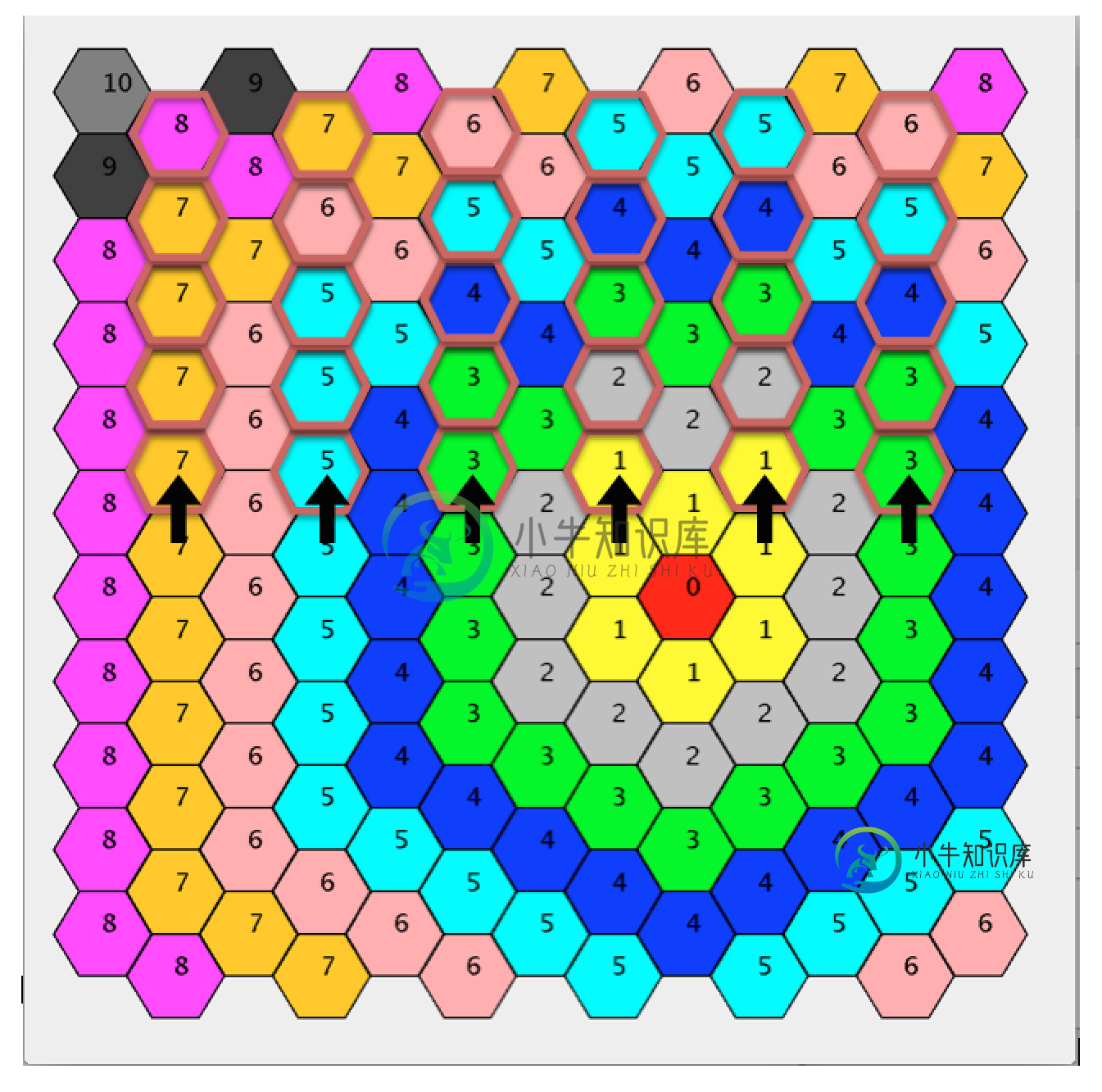
我要做的是找出在一个六角网格上,两点之间有多少个六边形。我试着在网上搜索一个公式,但我无法找到一个匹配类型的十六进制网格我正在使用。
-
我使用的是平顶六边形网格(按照这里列出的手册http://www.redblobgames.com/grids/hexagons/)。 当然,在平顶的情况下,x坐标可以用作x像素坐标。因此,从立方体坐标计算X像素坐标相对容易。假设是十六进制的总宽度,是x、y、z坐标数组,则x像素坐标为: 我不知道如何计算y像素坐标。相邻HEX之间的高度应不足等于。但是如何基于立方体坐标计算偏移量呢?
-
我有一个六边形网格,就像图中的一样,我试图找到最简单的方法(也许是一个公式)来计算这个网格内两个六边形之间的距离。当然,我的网格的大小比这更大,但是当我们计算规则网格(有水平和垂直轴)中两个节点之间的距离时,我试图找到一个类似于欧几里得距离公式的公式。 我读了一些方法,但他们都说Y轴应该是60度,然后他们提供了一些公式(六角网格中瓷砖之间的曼哈顿距离)。是否有一种方法来计算距离使用“坐标系”相同,
-
我需要计算汽车行驶的距离!不是距离,不是距离到否。如果我们通过谷歌提供的API计算,距离可以完全不同。谷歌可以提供从一个点到另一个点的1公里距离,但汽车可以按照骑手想要的方式行驶800米。使用加速计没有帮助。它适用于步行,但绝不适用于更快的速度。 我尝试过使用Google的位置API:距离到或距离之间根本不是一个选项。它可以给出与IN REAL截然不同的结果。在真实的汽车中,可以通过非常短的地方并
-
本文向大家介绍顶点之间的距离和偏心距,包括了顶点之间的距离和偏心距的使用技巧和注意事项,需要的朋友参考一下 两个顶点之间的距离 它是顶点U和顶点V之间最短路径中的边数。如果有多个路径连接两个顶点,则最短路径被视为两个顶点之间的距离。 表示法-d(U,V) 从一个顶点到另一顶点可以有任意数量的路径。其中,您只需要选择最短的一个即可。 示例 看一下下图- 在这里,从顶点“ d”到顶点“ e”或简称“

