无圈图的边加法
我有一个有向和无向边的图,现在我想通过用有向边替换它们来去掉无向边(每个无向边变成一个有向边)。每个无向边有两种可能性(用一个方向或另一个方向的有向边替换它)。
如何确定无向边的方向,使我的图保持无环(一个DAG)?
我的方法:
-
null
-
null
-
null

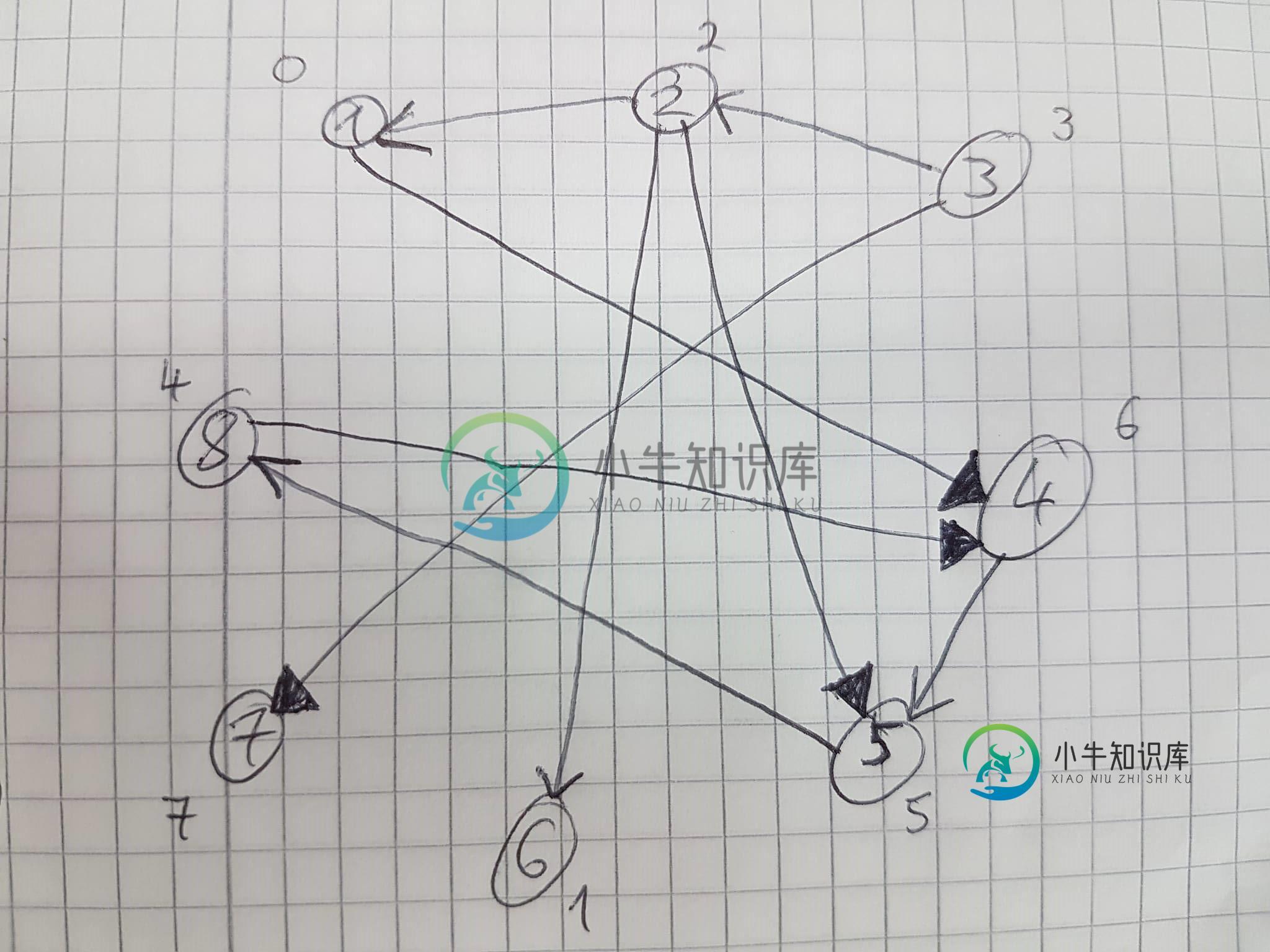
https://en.wikipedia.org/wiki/directed_acyclic_graph
共有1个答案
拓扑排序的定义是一个线性排序,每个线性排序都是一个总排序,所以从理论上讲,你的方法是很好的。但是,您的实现是错误的。
即。在你的拓扑顺序定义中,如果从a到b有一条边,那么b
-
在一个已执行DFS的无向图中(为了生成一个DFS树,从而将每条边分类为树边或后边),图中是否存在仅由后边组成的循环,即没有树边?
-
我正在编写一个使用电网格分析的程序。所以我有电路的节点[A,B,C,D]和连接节点[0,1,2,3,4,5,6,7,8]的分支。 如何在具有多条边的无向图中找到最短的循环? 图形图像(4个节点,9条边/分支): 周期: 我需要的循环数是:循环=分支-(节点-1),在本例中我需要6个循环。 我将这些数据存储在这样的数组中: 我很乐意看到任何语言的算法。
-
假设图G是一个有向无圈图,其顶点数为'n'no。如果我从图中移除所有边并使其完全断开,这会是一个DAG吗?
-
我有一个有向和无向边的图,现在我想通过用有向边替换它们来去掉无向边(每个无向边变成一个有向边)。每个无向边有两种可能性(用一个方向或另一个方向的有向边替换它)。
-
我正在寻找一种算法,它可以<编码>不同两个有向无环图(DAG)。也就是说,我想要一个算法,它在第一个DAG上产生删除和插入序列,以产生第二个DAG。 我不是百分之百确定,但我认为一个最长的公共子序列可以应用于DAG。我不太关心结果编辑序列的长度(只要它足够短),更关心算法的运行时间。 一个复杂的问题是,除了一个根节点之外,没有一个顶点被标记。根节点也是唯一一个内边为零的节点。图的边被标记,图中的“
-
请告诉我为什么这段代码不能分析无向图中是否有循环?代码如下。这是Spoj上的PT07Y问题。我正在做的是取一个节点并执行dfs。当执行dfs时,如果我访问同一个节点,那么我说有一个循环。从一个节点执行dfs后,我使访问的数组为假,并为下一个节点执行,直到我得到一个周期或所有节点都被访问。

