在图中查找循环（不一定是哈密顿的或访问所有节点）

Question

我有图1（第一个图像）中的一个图，并且希望连接红色节点以获得循环，但是循环不一定要像图2和图3（最后两个图像）那样是哈密顿的。这个问题比TSP有更大的搜索空间，因为我们可以访问一个节点两次。与TSP一样，不可能在一个大图中计算所有的组合，我应该尝试启发式，但问题是，与TSP不同，循环或巡回的长度在这里不是固定的。因为，访问所有的蓝色节点并不是强制性的，这导致包括一些蓝色节点在内的长度可变。如何每次生成一个可能的“有效”组合进行评估？我的意思是，一个循环可以是{a,e,B,l,k,j,D,j,k,C,g,f,e}或{a,e,B,l,k,j,D,j,I,h,g,C,g,f,e}，但不是{a,e,B,l,k,C,g,f,e}或{a,B,k,C,I,D}。

更新：最终目标是考虑长度和风险（见下文），评估哪个周期是最优/接近最优的。所以我不仅要把长度减到最小，而且要把风险减到最小。这就导致了如果不知道循环的所有节点顺序，就无法对循环的风险进行评估。希望这能澄清为什么我不能在新周期的生成过程中对其进行评估。我们可以：

• 逐个生成并评估可能的循环；
• 或生成所有可能的循环，然后对其进行计算。

风险定义：假设循环是连接主节点（其中一个红节点）到所有其他红节点的环。在环的任何部分（边缘）发生故障的情况下，不应将任何红色节点与主节点断开（这是希望的）。然而，有些边我们必须经过两次（由于没有连接所有红节点的哈密顿循环），如果这些边发生故障，有些红节点可能完全断开。因此循环风险是风险边的长度（我们在环/游中有两次）乘以在切掉每个风险边的情况下损失的红色节点数的总和。

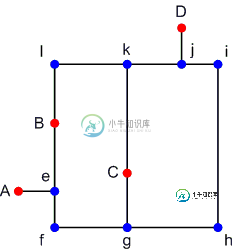
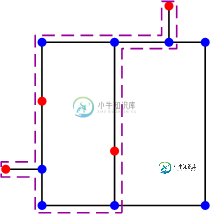
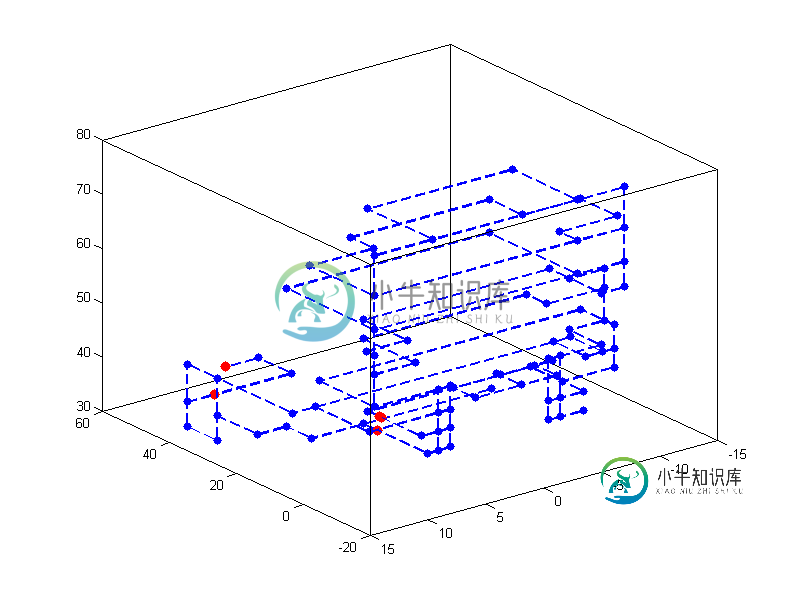
这里是Excel表的链接，其中包含上面图形的邻接矩阵（前五个节点是红色的，其余的是蓝色的）。

Answer 1

经过更多的思考，我决定重写我的解决方案可能更好，因为您可以使用红色节点两次，这使得我最初想要绘制红色节点之间的路径的想法效率低下。然而，它并不是完全浪费，因为红色节点之间的蓝色节点很重要。

实际上，您可以使用BFS的修改版本来解决这个问题，更多的是一种回溯算法。对于每个唯一分支，都存储了以下信息，其中大多数信息仅允许以更多空间为代价更快地拒绝，实际上只需要前两项：

• 完整的当前路径。（仅包含起始红色节点的列表）
• 剩余的红色节点。（最初为红色节点）
• 最后一个红色节点。（最初是开始红色节点）
• 自上一个红色节点以来的蓝色节点集。（最初为空）
• 计数为1的节点集。（最初为空）
• 计数为2的节点集。（最初为空）

该算法从单个节点开始，然后使用BFS或DFS扩展相邻节点，这一过程重复，直到结果是有效的旅行或待扩展的节点被拒绝。因此，基本的psudoish代码（当前路径和剩余红点）如下所示。其中rn是红色节点的集合，t是有效游览的列表，P/P2是节点的一条路径，R/R2是红色节点的集合，v是要扩展的节点，a是可能扩展到的节点。

function PATHS2HOME(G,rn)
    create a queue Q
    create a list t
    p = empty list
    v ← rn.pop()
    r ← rn
    add v to p
    Q.enqueue((p,r))
    while Q is not empty
        p, r ← Q.dequeue()
        if r is empty and the first and last elements of p are the same:
            add p to t
        else
            v ← last element of p
            for all vertices a in G.adjacentVertices(v) do 
                if canExpand(p,a)
                    p2 ← copy(p)
                    r2 ← copy(r)
                    add a to the end of p2
                    if isRedNode(a) and a in r2
                        remove a from r2
                    Q.enqueue( (p2,r2) )
    return t

以下情况会阻止节点的扩展。可能不是一个完整的列表。

• 红色节点：
  • 如果它在计数为2的节点集中。这是因为红色节点会被使用两次以上。
  • 如果等于最后一个红色节点。这防止了当一个红色节点与另外三个蓝色节点相邻时的“奇数”游览。因此，红色节点A与蓝色节点b、c和D相邻。然后您将结束一个巡回演出，巡回演出的一部分看起来像B-A-C-A-D。
  null
  null