如何在有向图的选定节点内找到循环？(C++)

Question

我目前正在研究一个在有向图中寻找由选定节点组成的圈的问题。

对于这里描述的实例：

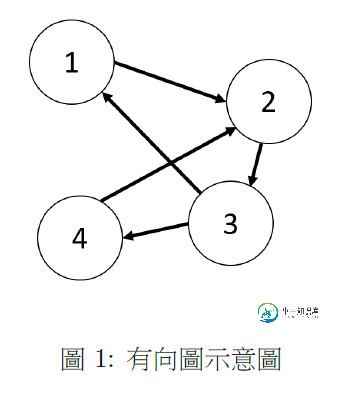
在节点1,2,3内有一个循环，在1,2,4内没有发现循环。我已经尝试用下面的操作来实现算法：

null

bool hasLoop(const int startNode, const bool directions[][MAX_DOT_NUM], const int nodesLen, bool nodesVisited[], const int selectedNodes[], const int selectedNum){
nodesVisited[startNode] = true;

for(int i = 0; i < nodesLen; i++){ //loop through all nodes 
    if(withinSelected(i, selectedNodes, selectedNum) == false) continue;  //check loop only for selected nodes
    if(directions[startNode][i] == 1){ //connected and is within selected nodes
        if(nodesVisited[i] == true){ 
            return true;                
        }else{
            if(hasLoop(i, directions, nodesLen, nodesVisited, selectedNodes, selectedNum)){
                return true;
            }
        }
    }
}
return false;

但是，这个实现并不适用来自我正在使用的在线判断的所有测试数据。我发现我的算法不同于深度优先搜索，深度优先搜索使用白、灰、黑数组来存储未访问、正在访问或不需要访问的节点，我想知道这是否是导致问题的原因。

希望在您的帮助下，我能找到导致此实现不适用于所有情况的bug！非常感谢你阅读这篇文章！

编辑：这是一个有向图！对此很抱歉。

bool hasLoop(const int currentNode, const bool directions[][MAX_DOT_NUM], const int nodesLen, bool nodesVisited[], const int selectedNodes[], const int selectedNum, const int startNode){
// cout << currentNode << " -> ";
nodesVisited[currentNode] = true;

for(int i = 0; i < nodesLen; i++){
    if(withinSelected(i, selectedNodes, selectedNum) == false) continue;
    if(directions[currentNode][i] == 1){ //connected and is within selected nodes
        if(nodesVisited[i] == true){ 
            if(i == startNode) return true;        
        }else{
            if(hasLoop(i, directions, nodesLen, nodesVisited, selectedNodes, selectedNum, startNode)){
                return true;
            }
        }
    }
}
return false;

Answer 1

您的实现是一个DFS，但对于不创建循环的“侧节点”将失败：

考虑有3个节点的图(A，B，C):

      A
    /   \
   /     \
  V       V
  B <---- C

你的算法会告诉图有一个循环，而事实上-它没有！

在这两种解决方案中，只在包含“选定节点”的子图上应用算法。这两种解决方案都是O(V+E)时间和O(V)空间。