解决圆-圆碰撞

Question

我正在编写软件，扩展圆-矩形碰撞检测（交集），以包括对碰撞的响应。圆边和圆矩形是相当直接的。但一圈又一圈地把我难住了。

例如，在离散事件模拟中，让两个圆碰撞，一个红一个绿。我们可能会出现以下情况：

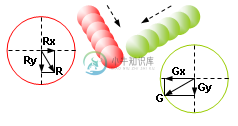
在它们碰撞后，我们可以立即：

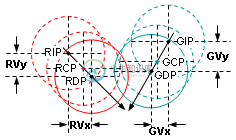
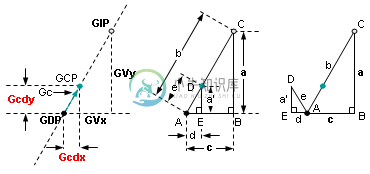
这里的RIP和GIP是在前一个时钟滴答的圆圈的位置。在当前时钟滴答时，在RDP和GDP处检测到冲突。然而，当两个圆位于RCP和GCP时，碰撞发生在时钟滴答之间。在时钟滴答声中，红色圆圈向下移动RVy，向右移动RVx；绿色圆圈向下移动GVy，向左移动GVx。RVy不等于GVY；RVx也不等于GVx。

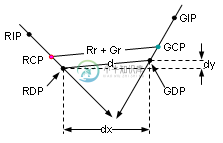
当圆心之间的距离小于或等于圆的半径之和时，即在上图中，d<=(Rr+Gr)就会发生碰撞。在d<(Rr+Gr)的碰撞中，我们需要在调整圆的速度分量之前将DPs定位回CPs。在d==(Rr+Gr)的情况下，不需要重新定位，因为DP位于CPS处。

这就是问题所在：我如何回到CPS。一些作者建议应用一半的穿透力，下图中由p给出。

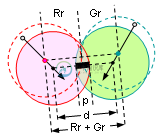
对我来说那是完全错误的。它假设两个圆的速度矢量相等，但在本例中并非如此。我认为穿透力与计算有关，但我不知道如何穿透力。我知道这个问题可以被重铸为一个我们想要为Gcdy和gcdx解决的右相似三角形的问题。

碰撞本身将被模拟为弹性的，而惯量交换的数学方法已经到位。唯一的问题是在碰撞时把圆圈放在哪里。

Answer 1

“这就是问题所在：我该如何行动。”

很可能你想知道“在调整圆圈的速度分量之前，如何将DPs定位回CPs。”

所以有两个问题，如何确定CPs（碰撞发生的地方），以及如何从那个点开始调整圆圈的运动。第一部分有一个相当容易的解法（考虑到不同的半径和速度分量），但第二部分取决于模拟的是弹性响应还是非弹性响应。你在评论中写道：

碰撞将被模拟为弹性的。惯性交换的数学方法已经就绪。问题是把圆圈放在哪里。

考虑到我将只讨论第一个问题，解决碰撞发生的确切位置。假设两个圆都作匀速运动，只要知道碰撞发生的确切时间就足够了，即当两个圆的圆心之间的距离等于它们的半径之和时。

在匀速运动中，人们可以把一个圆（红色）的速度减去另一个圆（绿色）的速度，将其视为静止不动。实际上，我们把第一个圆的中心视为固定的，而只认为第二个圆是（匀速）运动的。

现在通过求解一个二次方程来求出碰撞的精确时间。设V=(GVx-RVx,GVy-RVy）是圆的相对运动,P=(GIPx-RIPx,GIPy-RIPy）它们在碰撞前“瞬间”的相对位置。我们通过定义以下内容来“动画”相对位置P的线性路径：

P(t)=P+t*V

并询问这条直线何时与围绕半径RR+GR原点的圆相交，或者何时相交：

（Px+T*Vx)^2+（Py+T*Vy)^2=（Rr+Gr）^2

这是一个未知时间t的二次方程，所涉及的所有其他量都是已知的。在这种情况下（碰撞发生在位置CP处或之前）将存在一个正的实解（通常有两个解，一个在位置CP之前，一个在位置CP之后，但可能有一个给出“双根”的掠接触）。您想要的解（根）t是较早的一个，即t（在“瞬时”RIP和GIP位置为零）较小的一个。