去除最小边数以断开图中两个顶点的连接
在这里,我试图断开图中的两个顶点,尽可能减少边的去除。
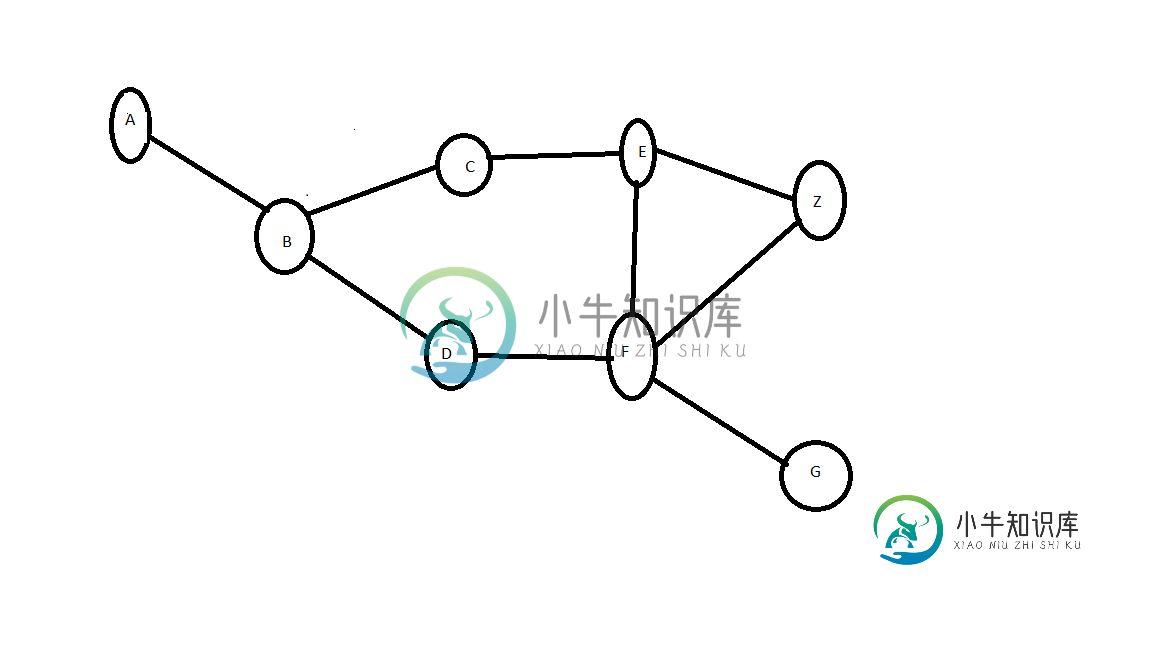
对此有没有具体的算法?
我找到了一些用最大流最小割问题来解决这一问题的建议,但我还没有得到将这一问题转化为最大流最小割定理的一般思想。同样,在这个过程中,我可能会在F和G之间去掉一条边,这是无用的。
共有1个答案
这可以用最大流量-最小切割问题来解决。
您可以将图建模为网络流,如下所示:
1。将A视为源顶点,Z视为接收器顶点。
2。将每个边沿的容量设置为1个单位。
现在,解决了上述网络中的最大流量-最小割集问题。使用它,您将能够找到从A到Z的多条边不相交的路径。对于每个这样的路径,删除第一个边(源自源A的边)。
-
我想知道是否有人能帮我,我遇到了一个问题,在spark中为graphx编写的函数,如果我有没有边的顶点,它总是给出错误消息。
-
我如何从这样的图中删除所有的循环?所有的边长度都是一个,所有的边要么是垂直的,要么是水平的。图是连通的。 我想计算为了使图不包含圈而必须去除的边的最小数目。 如果包含示例代码(最好是C++、C或Java),将会非常有帮助。 更新:显然我必须找到顶点和边的数量。我的问题给出了一组类似(向下、向左、向上、向下、向左、向左、向上、向下)的指令。你从坐标平面中的(0,0)开始,在指定的方向上移动一个单位。
-
这是史蒂文·斯基纳(StevenSkiena)提出的算法设计问题(用于面试准备): 图G的一个连接点是一个顶点,其删除与G断开。设G是一个有n个顶点和m条边的图。给出一个简单的O(n m),该O(n m)可以为n个顶点找到一个删除顺序,以便没有删除会断开图形。 这就是我的想法: > 在图上运行DFS并不断更新每个节点最古老的可达祖先(我们根据它来决定它是桥切节点、父可爱节点还是根切节点) 如果我们
-
我正在寻找一个算法,找到顶点的最小子集,这样从图中移除这个子集(以及连接这些顶点的边),所有其他顶点都变得不连通(即,图将没有任何边)。 null 我有图论的基础知识,所以请原谅任何不正确的地方。
-
上面的代码将“浮点值”打印为12345678,我需要12345678.12 我怎样才能得到我的结果?请让我知道。
-
我有一个无向连通图,我想通过移除顶点而不是边来隔离它的所有顶点,我想保持我移除的顶点数量最小。我知道要实现这一点,我必须每次移除程度最高的顶点,直到图断开。但是我需要为它写一个Java的程序,我不知道如何跟踪程度最高的顶点以及使用哪种数据结构。我得到了以下输入。 :分别表示顶点和边的数量。 :指定边的顶点对 样本输入: 示例输出:(这是需要删除的最小数量的顶点,使顶点隔离) 限制条件:

