在无向连通图中,如何找到一组顶点集,除去图的不连通点?
我知道在无向连通图中关节点是一个顶点,去掉后图就断开了。对于Java代码,我访问了以下链接http://algs4.cs.princeton.edu/41undirected/biconnected.Java.html。
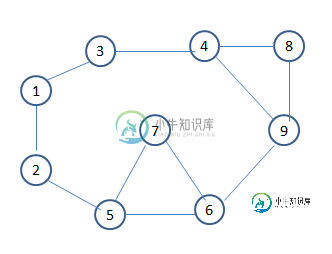
在上面的图中没有连接点,因为图不会因为去掉任何一个顶点而断开连接。但是我们可以通过移除一个以上的顶点来使图断开连接,例如,如果我们移除4、6个顶点,图就会断开连接。
如何找到一组顶点,这样在去掉那些顶点后,图就变得断开了。假设可以删除的顶点有极限,它是3个。这意味着我们不能一次删除超过3个顶点来使图断开连接。
我在想-
步骤1-运行算法以找到单个连接点。
步骤2-如果在步骤1之后没有连接点,我们从图中移除一个顶点并运行连接点算法,我们对图中的所有顶点执行此操作。使用这个我们可以找到两个顶点(第一个是在运行algo之前被移除的顶点,第二个是在运行algo之后被找到的顶点),它们的移除将使图形断开连接,程序将停止,因为我们已经找到了一组顶点。
如何找到最小顶点集删除后,图变得断开。
什么是找到顶点集的更好的方法,除去图变得断开。
共有1个答案
对于任何度数(即邻居计数)为d的顶点,去除其所有的d个邻居将断开图的连接(除非那些是图中唯一的其他顶点)。这样就给出了需要删除的顶点数量的上限,以及为了达到这个上限可以删除的实际顶点:只需寻找一个度数最小的顶点,然后删除它的所有邻居。
在您的示例图中,您知道这是最优解,因为有度为2的顶点,并且您已经排除了大小为1的解,因为您发现该图是双连接的(即,不包含连接点)。然而,一般而言,可能比这个上界做得更好:例如,考虑一个由k个顶点上的团的2个拷贝,加上2条附加边(u1,v1)和(u2,v2)组成的图,第一个团有u1和u2,第二个团有v1和v2。即使可以使最小度k任意大,也可以通过仅删除u1和u2(或仅删除v1和v2)来断开连接。
-
我如何从这样的图中删除所有的循环?所有的边长度都是一个,所有的边要么是垂直的,要么是水平的。图是连通的。 我想计算为了使图不包含圈而必须去除的边的最小数目。 如果包含示例代码(最好是C++、C或Java),将会非常有帮助。 更新:显然我必须找到顶点和边的数量。我的问题给出了一组类似(向下、向左、向上、向下、向左、向左、向上、向下)的指令。你从坐标平面中的(0,0)开始,在指定的方向上移动一个单位。
-
我正在努力自学图论,现在试图理解如何在图中找到SCC。我读过关于SO的几个不同的问题/答案(例如,1、2、3、4、5、6、7、8),但我找不到一个可以遵循的完整的一步一步的例子。 根据CORMEN(算法导论),一种方法是: 调用DFS(G)计算每个顶点u的完成时间f[u] 计算转置(G) 调用DFS(转置(G)),但在DFS的主循环中,按F[u]递减的顺序考虑顶点(如步骤1中计算的那样) 输出步骤
-
我想在无向图中找到一个强连通分量,即如果我从一个节点开始,那么我将回到节点,并且每个边都被精确地访问一次。 对于有向图,可以用Tarjan算法求强连通分量,但是对于无向图,该怎么办。
-
有没有一种算法可以高效地找到这个中心?理想情况下,性能只取决于及其周围环境,而不取决于整个图。 我考虑过从中的所有顶点同时开始广度优先搜索,当所有遇到一个顶点时停止搜索,但这并不是太高效。在这种情况下可能是可行的,但感觉可能有更好的方法。
-
背景:我是图论的新手,特别是“图割”。请不要太技术和速度。谢谢。 假设我有一个加权无向连通图G=(V,E)。我有一个变量a,它包含一个整数值,我想从图G中删除/裁剪所有权重低于a值的边。 问题1:如果图论中已经存在这一点(我看到了max-cut、min-cut、s-t cut,等等),它怎么称呼? 问题2:我如何使用数学符号正式表达/定义这种方法。 谢谢你的建议。
-
根据CLRS第3版的定义,单连通有向图是指每对顶点(u,v)至多有一条唯一的路从u->v来的图。现在我读过的大多数答案都说,我们从图中的每个顶点运行DFS,如果在任何情况下我们找到一条交叉边或一条前向边,那么图就不是单连通的。我可以理解前向边的概念,但是在这个图上运行这个algo 1-->2<--3将给出一个结果:它不是单连通的,而这个图是单连通的。我们有一个从3->2或1->2的交叉边,这取决于

