如何在图中找到强连通分量？

Question

我正在努力自学图论，现在试图理解如何在图中找到SCC。我读过关于SO的几个不同的问题/答案（例如，1、2、3、4、5、6、7、8)，但我找不到一个可以遵循的完整的一步一步的例子。

根据CORMEN（算法导论），一种方法是：

1. 调用DFS(G)计算每个顶点u的完成时间f[u]
2. 计算转置(G)
3. 调用DFS（转置(G))，但在DFS的主循环中，按F[u]递减的顺序考虑顶点（如步骤1中计算的那样）
4. 输出步骤3的深度优先森林中每棵树的顶点作为单独的强连通分量

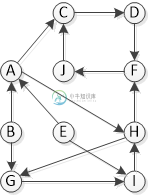
从顶点A开始运行DFS：

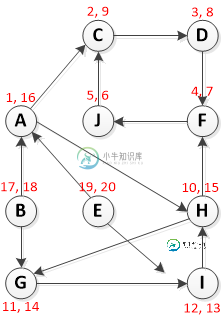
请注意红色文本格式为[访问前，访问后]

步骤2：计算转置(G)

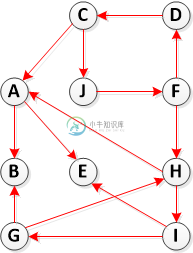
null

所以我们有五个强连通分量：{E},{B},{A},{H,I,G},{C,J,F,D}

Answer 1

您的步骤是正确的，您的答案也是正确的，通过检查您提供的其他答案，您可以看到他们使用了一个不同的算法：首先，您对G转置运行DFS，然后您对G运行一个无向组件算法，从上一步开始，按照顶点的投递数递减的顺序处理顶点。

问题是，他们在G上执行最后一步，换位而不是在G中，因此得到了一个不一致的答案。如果你从第98页开始阅读Dasgupta，你会看到他们（试图）使用的算法的详细解释。