LeetCode 241的时间和空间复杂度是多少。添加括号的不同方法？

Question

我试图理解什么是leetcode 241的时间复杂性。添加括号的不同方式。我用了回忆录技术。我的朋友被问到在谷歌编码轮，他不能给出正确的时间和空间复杂度。我在Leetcode中也发现了同样的问题。

问题：给定一串数字和运算符，返回所有可能的结果，从计算所有不同的可能方法，以分组数字和运算符。有效运算符是+、-和*。

例1：

((2-1)-1)=0

(2-(1-1))=2

例2：

说明：

(2*(3-(4*5)))=-34

((23)-(45))=-14

import java.util.*;

class Solution {
    Map<String, List<Integer>> map = new HashMap<>(); 
    public List<Integer> diffWaysToCompute(String input) {
        if(map.containsKey(input)) {
            return map.get(input);
        }
        
        List<Integer> result = new ArrayList<>();
        int length = input.length();
        
        for(int i = 0; i< length; i++) {
            char character = input.charAt(i);
            if(isOperator(character)) {
                String part1 = input.substring(0, i);
                String part2 = input.substring(i + 1);
                List<Integer> part1Result = diffWaysToCompute(part1);
                List<Integer> part2Result = diffWaysToCompute(part2);
                computeAndStoreResult(input, result, i, part1Result, part2Result);
        
            }
        }
        //store in map...
        map.put(input, result);
        //this is when only one input is present. 
        // input 3 ==> nothing is added in result so add 3 ...
        if(result.size() == 0) {
            result.add(Integer.valueOf(input));
        }
        return result;
    }
    
    private boolean isOperator(char character) {
        return character == '-' || character == '*' || character == '+';
    }
    
    private void computeAndStoreResult(String input, List<Integer> result, int i, List<Integer> part1Result, List<Integer> part2Result) {
        for(Integer p1 : part1Result) {
            for(Integer p2 : part2Result) {
                int c= 0;
                switch (input.charAt(i)) {
                    case '+':
                        c = p1+p2;
                        break;
                    case '-':
                        c = p1-p2;
                        break;
                    case '*':
                        c = p1*p2;
                        break;
                }
                result.add(c);
            }
        }
    }
}

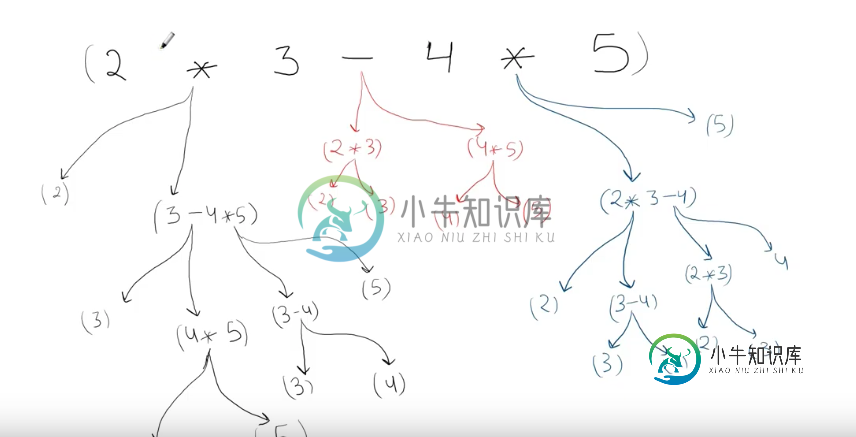
https://just4once.gitbooks.io/leetcode-notes/content/leetcode/divide-and-conquer/241-不同的-ways-to-add-parenthes.html

Answer 1

1. 如果表达式由单个数字组成，则有1放置圆括号的方法。
2. 如果表达式中只有1数学运算符，那么只有1放置圆括号以获得相关结果的方法。例如，对于3+4，它是(3+4).
3. 如果表达式中有2数学运算符，则有2放置圆括号的方法。例如，对于3+4-2，该方法将通过+将表达式拆分为3和4-2，然后通过-将表达式拆分为3+4和2。所以，它是2方式。
4. 如果表达式中有3数学运算符，则为5结果。例如，1+2-3*4可以拆分为1和2-3*4、1+2和3*4、1+2-3和4。我们从2）和3）中了解到，ways的数量是2+1+2=5`ways.
5. 如果表达式中有4数学运算符，则为14结果。例如，1+2-3*4+5可以拆分为1和2-3*4+5、1+2和3*4+5、1+2-3*4和5。正如我们从2)、3)和4）中学到的，方法的数量是5+2+2+5=14ways。

如果继续这个序列，那么它将是42、132、429、1430、4862、16796、58786、208012、742900、...。如你所见，它呈指数增长。

这样的数字序列有一个名字，叫做加泰罗尼亚数字。

正如您可能已经意识到的那样，即使在您获得由第一个数学运算符拆分的左子表达式和右子表达式的结果后，您的算法也将变得指数化。

因此，如果有10数学运算符，那么在计算第一个配置的结果（表达式被第一个数学运算符拆分）之后，它们的数目将是4862。

所以，不仅你的时间复杂度是指数的，而且你的空间复杂度，因为你把所有的结果都保存在一个列表中。