生成Mandelbrot分形时，如何设置c的值？

Question

生成Mandelbrot分形的方程是Zn1=Zn^2 C。问题是，在计算机程序中，C用于屏幕上的缩放/分辨率和位置。我的问题是，我怎样才能得到这样的分形：

沃尔夫拉姆

（方程f（z）=sin（z/c），z0=c）

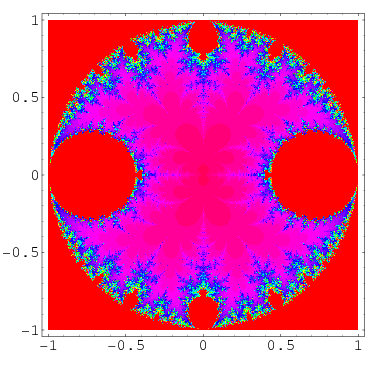
我的代码（来自罗塞塔代码）：

public class MandelbrotSet extends JFrame {
    private static final long serialVersionUID = 5513426498262284949L;
    private final int MAX_ITER = 570;
    private final double ZOOM = 150;
    private BufferedImage image;
    private double zx, zy, cX, cY, tmp;

    public MandelbrotSet() {
        super("Mandelbrot Set");
        setBounds(100, 100, 800, 600);
        setResizable(false);
        setDefaultCloseOperation(EXIT_ON_CLOSE);
        image = new BufferedImage(getWidth(), getHeight(), BufferedImage.TYPE_INT_RGB);
        for (int y = 0; y < getHeight(); y++) {
            for (int x = 0; x < getWidth(); x++) {
                zx = zy = 0;
                cX = (x - 400) / ZOOM;
                cY = (y - 300) / ZOOM;
                int iter = MAX_ITER;

                while (zx * zx + zy * zy < 4 && iter > 0) {
                    tmp = zx * zx - zy * zy + cX;
                    zy = 2.0 * zx * zy + cY;
                    zx = tmp;
                    iter--;
                }

                image.setRGB(x, y, iter | (iter << 8));
            }
        }
    }

        @Override
        public void paint(Graphics g) {
            g.drawImage(image, 0, 0, this);
        }

    public static void main(String[] args) {
        new MandelbrotSet().setVisible(true);;
    }
}

Answer 1

利用三角定理

sin(A+i*B)=sin(A)*cos(i*B)+  cos(A)*sin(i*B) 
          =sin(A)*cosh(B )+i*cos(A)*sinh(B )

对于商，使用z=xi*y和c=ai*b

(x+i*y)/(a+i*b)=(x+i*y)*(a-i*b)/(a*a+b*b)

对于上面的正弦表达式

A = (a*x+b*y)/(a*a+b*b)
B = (a*y-b*x)/(a*a+b*b)

在javascript中，生成此分形的小脚本可以如下所示：

function cosh(x) { return 0.5*(Math.exp(x)+Math.exp(-x)); }
function sinh(x) { return 0.5*(Math.exp(x)-Math.exp(-x)); }

function rgb(r,g,b) { return "rgb("+r+","+g+","+b+")"; }
var colors = new Array(24);
for(var k=0; k<8; k++) {
    colors[   k] = rgb(k*64,(7-k)*64,(7-k)*64);
    colors[ 8+k] = rgb((7-k)*64,k*64,(7-k)*64);
    colors[16+k] = rgb((7-k)*64,(7-k)*64,k*64);
}

var cvs = document.getElementById('sine-fractal');
var ctx = cvs.getContext('2d');
var cx = 0.0, cy = 0.0;
var dx = 1.0;

var tiles = 100;
var scale = Math.min(cvs.width, cvs.height) / tiles;
ctx.scale(scale, scale);

function localx(i) { return cx-dx + 2*i*dx/tiles; }
function localy(j) { return cy-dx + 2*j*dx/tiles; }

for (var i = 0; i < tiles; i++) {
  var a = localx(i);
  for (var j = 0; j < tiles; j++) {
    var b = localy(j);
    var r2 = a*a + b*b;
    var x = a, y = b;
    var rounds = 0;
    var max = 500;
    while (x * x + y * y < 4 && rounds < max) {
      var u = (a*x + b*y) / r2, v = (a*y - b*x) / r2;
      x = Math.sin(u) * cosh(v);
      y = Math.cos(u) * sinh(v);
      rounds++;
    }
    ctx.fillStyle = colors[rounds % 24];
    ctx.fillRect(i, j, 1, 1);
  }
}

<canvas id='sine-fractal' width=200 height=200></canvas>