在有向加权图中求两个节点之间的最短路径
我有一个有向加权图G=
路径重量=此路径中最重的两条边。
因此,经典的Dijkstra算法和修改的二进制堆不起作用。我想,我必须修改这个算法。我正在努力,但没有成功。
示例。
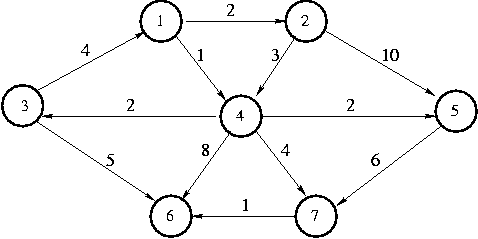
3和5=4 2=6之间的路径权重
3和7=4=8之间路径的权重
共有1个答案
根据David Eisenstat的反例编辑了我的答案。
你在问题中给出的例子不是Dijkstra何时不起作用的好例子。
我相信你可以通过修改Dijkstra来做到这一点。关键是跟踪每个顶点的多个备选方案。你不仅需要存储组成最短路径的重量,还需要存储最大路径的替代品
Dijkstra是贪婪的,所以你必须弄清楚的是:一旦确定了一条最短路径,是否有可能找到另一条更短的路径。因为您将发现越来越长的路径,所以这是不可能的。
-
我需要帮助在一个未加权无向图中找到两个节点之间的所有最短路径。 我能够使用BFS找到一条最短路径,但到目前为止,我还不知道如何找到并打印出所有路径。 知道我可以使用的算法/伪代码吗?
-
我正在寻找最有效的算法,根据大O符号,在未加权有向图中找到两个节点之间的最短路径。 我主要分为带堆的Dijkstra和呼吸优先搜索,如果图加权,我通常会使用堆。 在这种情况下,未加权的图是否会使Dijkstra的使用效率低于BFS?
-
在无向赋权图中寻找两个顶点之间的最短路径。还已知权重是小于log(logV)的整数,其中V是顶点的数量。使用贝尔曼-福特或Dijkstra算法很容易解决,但是有没有什么算法可以更快地解决呢? 到目前为止,我一直在考虑使用BFS,将权重大于1的边划分成两个权重为1的边,但如果V是大数,就不是一个好主意。不,这不是我的家庭作业,我只是在想。
-
以下是练习: null null 我的算法正确吗?如果我做v到w,然后做w到v,这仍然被认为是线性时间吗?
-
在一个加权有向图中,我需要找到两个结点s,t之间的最短路径。以下是限制: 权重可以为负值。 路径必须经过一个特定的边,让我们从节点u到V调用her e和shes。 输出路径必须简单,即我们只通过一个节点一次。 因为我希望它最短,所以我将检查在从s到u之前从v到t运行bellman ford是否比相反的方式更快(如果有节点,两个节点都使用where是放置它的最佳位置)。 谢谢你的帮助!
-
我有一个有向加权图G,其中权重是过渡的持续时间。 我使用DFS编写了两个顶点之间的所有路径搜索算法,并进行了修改:搜索将继续,直到路径的总权重(其各部分的权重之和)小于某个值。 我的代码在小图中工作,但在大图中(| V |=1800,| E |=50870)它会冻结。

