“解码”正弦泰勒级数近似值

Question

我使用泰勒级数来计算< code>sin()。对原罪的泰勒级数是:

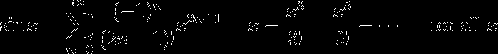
我使用的实现如下所示:

float sine(float x, int j)
{
    float val = 1;

    for (int k = j - 1; k >= 0; --k)
        val = 1 - x*x/(2*k+2)/(2*k+3)*val;

    return x * val;
}

据我所知，该代码是多项式的j项的近似（换句话说，该近似是从零到j的求和，而不是从零到∞), k在公式中是n，当然x 。

我在努力理解那个实现，也就是从上面的公式到代码的转换。我的目标是为< code>cos()系列编写相同类型的实现。

你能帮我理解一下吗？

Answer 1

这是一个麦克劳林级数，但它的编写是为了减少使用级数一般项的递推公式进行计算的次数。

余弦的版本如下（连同简单的测试线束）：

#include <stdio.h>
#include <math.h>

float cosine(float x, int j)
{
    float val = 1;
    for (int k = j - 1; k >= 0; --k)
        val = 1 - x*x/(2*k+2)/(2*k+1)*val;
    return val;
}

int main( void )
{
    for( double x = 0.0; x <= 1.57; x += 0.1 )
    {
        printf("%10g    %10g    %10g\n", x, cos(x), cosine(x, 5));
    }
    return 0;
}

EDIT（用LaTeX创建的图像替换丑陋的文本数学）

为了理解这个技巧，让我们把重点放在< code>sine的例子上，回忆一下正弦函数的McLaurin展开式:

现在让我们展开到第5项(N=5)，忽略余数R，进行一些重写，包括x²项的因式分解。下面描述了产生的步骤，其中重写的子表达式用方括号中的数字标记:

C函数只是这种自下而上的递归重写的实现，也就是说，在上述模式中作为最后一步出现的内容首先在< code>sine函数中进行计算(该示例与< code>j==4的调用相关，因此循环变量< code>k从值< code>3开始，一直到< code>0)。