利用置换矩阵进行稀疏矩阵的Cholesky分解

Question

我对大型稀疏矩阵的Cholesky分解感兴趣。我遇到的问题是，Cholesky因子不一定是稀疏的（就像两个稀疏矩阵的乘积不一定是稀疏的）。

例如，对于仅沿第一行，第一列和对角线具有非零的矩阵，Cholesky因子具有100%的填充（下三角形和上三角形是100%的密度）。在下面的图像中，灰色为非零，而白色为零。

我知道的一个解决方案是，找到一个置换P矩阵，然后对psupt/supap进行Cholesky分解。例如，对于相同的矩阵，通过应用将第一行移动到最后一行，将第一列移动到最后一列的置换矩阵，Cholesky因子是稀疏的。

我的问题是一般如何确定P？

要从一个更真实的矩阵中了解A和PSUPT/SUPAP的Cholesky分解的区别，请看下面的图像。我从http://www.seas.ucla.edu/vandenbe/103/lectures/chol.pdf上获取了所有这些图像

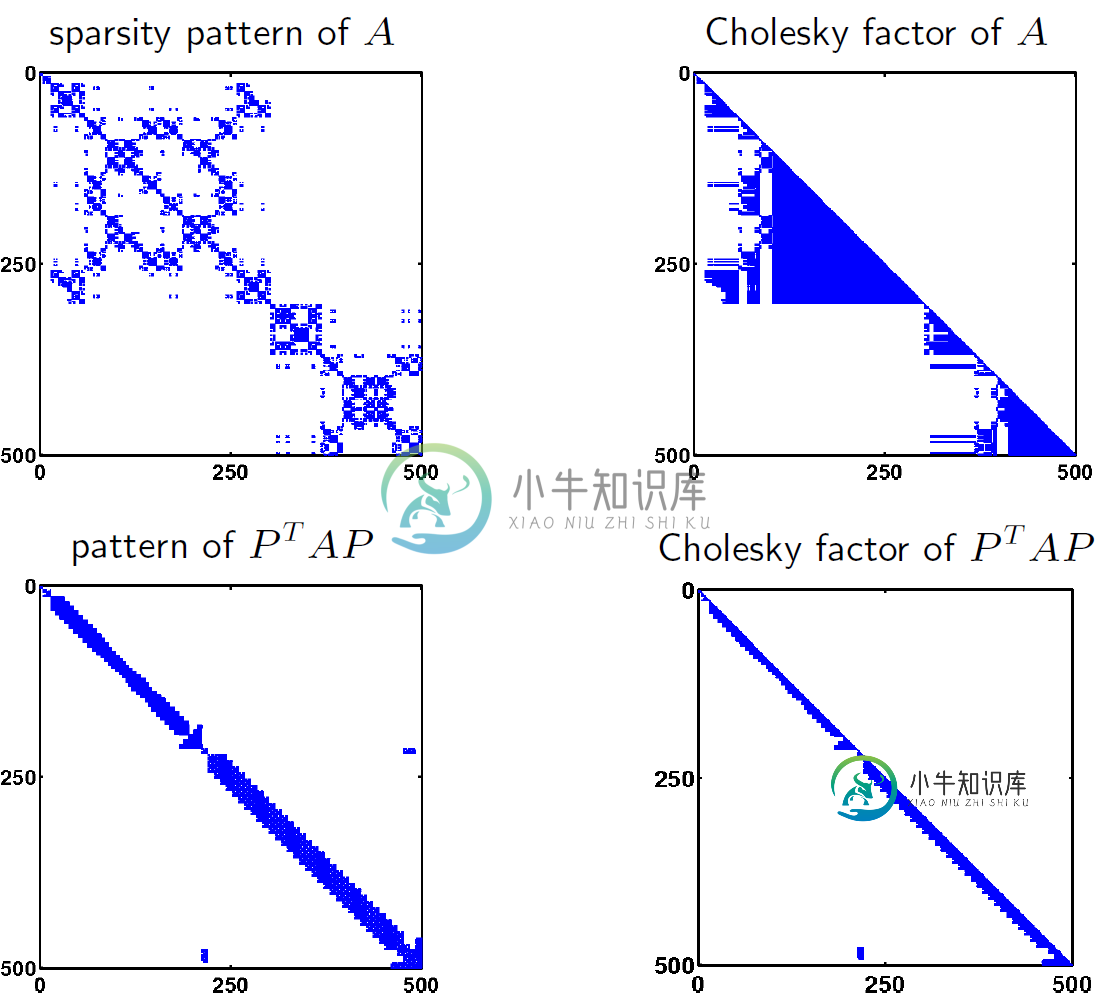
根据课堂讲稿

有许多启发式方法（我们没有讨论）来选择好的置换矩阵P。

我想知道其中的一些方法是什么（用C，C++，甚至Java编写的代码会是理想的）。

Answer 1

求矩阵的行和列的最佳排列以求最小填充矩阵因子分解的问题并不是一个简单的问题（如评注中所指出的）。因此，启发式算法在实际应用中得到了应用。

有一些库实现启发式重编号/排序策略，通常基于矩阵邻接图的图算法。一个是尽量减少相应邻接矩阵的带宽。一种易于实现的算法是Cuthill-McKee算法或最小度排序算法。关于这个问题的更多信息可以在Yousef Saad:Iterative Methods for Sparse Linear Systems（2003）一书中找到。

许多库实现了启发式算法，例如

中实现的排序html" target="_blank">方法 boost.graph直接处理邻接图，并提供了一些排序算法，如Cuthill-McKee和Minimum-dex ordering/li>

其中一些库还提供了稀疏的Cholesky分解方法，可以直接使用。