DNN的梯度更新方式
参考回答:
1)批量梯度下降法BGD
批量梯度下降法(Batch Gradient Descent,简称BGD)是梯度下降法最原始的形式,它的具体思路是在更新每一参数时都使用所有的样本来进行更新,其数学形式如下:
(1) 对上述的能量函数求偏导:
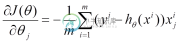
(2) 由于是最小化风险函数,所以按照每个参数的梯度负方向来更新每个:

2)随机梯度下降法SGD
由于批量梯度下降法在更新每一个参数时,都需要所有的训练样本,所以训练过程会随着样本数量的加大而变得异常的缓慢。随机梯度下降法(Stochastic Gradient Descent,简称SGD)正是为了解决批量梯度下降法这一弊端而提出的。
将上面的能量函数写为如下形式:
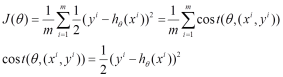
利用每个样本的损失函数对求偏导得到对应的梯度,来更新:
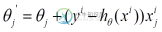
3)小批量梯度下降法MBGD
有上述的两种梯度下降法可以看出,其各自均有优缺点,那么能不能在两种方法的性能之间取得一个折衷呢?即,算法的训练过程比较快,而且也要保证最终参数训练的准确率,而这正是小批量梯度下降法(Mini-batch Gradient Descent,简称MBGD)的初衷。
-
本文向大家介绍梯度消失,梯度爆炸的问题,相关面试题,主要包含被问及梯度消失,梯度爆炸的问题,时的应答技巧和注意事项,需要的朋友参考一下 参考回答: 激活函数的原因,由于梯度求导的过程中梯度非常小,无法有效反向传播误差,造成梯度消失的问题。
-
方向导数 定义:若二元函数$$z=f(x,y)$$在点$$P(x_0,y_0)$$处沿着$$\vec{l}$$(方向角为$$\alpha$$,$$\beta$$)存在下列极限 $$ \dfrac{\partial f}{\partial l}=\lim\limits_{\rho\to 0}\dfrac{f(x+\Delta x, y+\Delta y)-f(x,y)}{\rho} $$ $$ =f
-
我如何在JavaFX中开发一个类似下面的渐变?
-
在本节中,我们将介绍梯度下降(gradient descent)的工作原理。虽然梯度下降在深度学习中很少被直接使用,但理解梯度的意义以及沿着梯度反方向更新自变量可能降低目标函数值的原因是学习后续优化算法的基础。随后,我们将引出随机梯度下降(stochastic gradient descent)。 一维梯度下降 我们先以简单的一维梯度下降为例,解释梯度下降算法可能降低目标函数值的原因。假设连续可导
-
本文向大家介绍梯度消失相关面试题,主要包含被问及梯度消失时的应答技巧和注意事项,需要的朋友参考一下 参考回答: 在神经网络中,当前面隐藏层的学习速率低于后面隐藏层的学习速率,即随着隐藏层数目的增加,分类准确率反而下降了。这种现象叫做消失的梯度问题。
-
我使用的是内核密度估计(KDE)的SciPy实现(http://docs.SciPy.org/doc/SciPy/reference/generated/SciPy.stats.gaussian_kde.html),到目前为止工作良好。然而,我现在想要获得KDE在一个特定点的梯度。 我已经查看了库的Python源代码,但还没有弄清楚如何轻松实现这个功能。有人知道这样做的方法吗?

