推导LSTM正向传播和单向传播过程
参考回答:
前向推导过程:

反向推导过程:
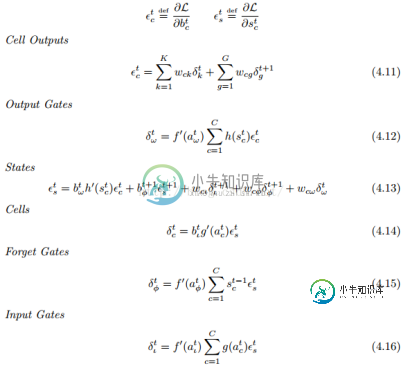
-
前面几节里我们使用了小批量随机梯度下降的优化算法来训练模型。在实现中,我们只提供了模型的正向传播(forward propagation)的计算,即对输入计算模型输出,然后通过autograd模块来调用系统自动生成的backward函数计算梯度。基于反向传播(back-propagation)算法的自动求梯度极大简化了深度学习模型训练算法的实现。本节我们将使用数学和计算图(computationa
-
在RNN模型里,我们讲到了RNN具有如下的结构,每个序列索引位置t都有一个隐藏状态h^{(t)}。 如果我们略去每层都有的$$o{(t)}, L{(t)}, y^{(t)}$$,则RNN的模型可以简化成如下图的形式: 图中可以很清晰看出在隐藏状态$$h{(t)}$$由$$x{(t)}$$和$$h{(t-1)}$$得到。得到$$h{(t)}$$后一方面用于当前层的模型损失计算,另一方面用于计算下一层
-
卷积神经网络其实是神经网络特征学习的一个典型例子。传统的机器学习算法其实需要人工的提取特征,比如很厉害的SVM。而卷积神经网络利用模板算子的参数也用以学习这个特点,把特征也学习出来了。其实不同的模板算子本质上就是抽象了图像的不同方面的特征。比如提取边缘,提取梯度的算子。用很多卷积核去提取,那就是 提取了很多的特征。一旦把参数w,b训练出来,意味着特征和目标之间的函数就被确定。今天分享下CNN的关键
-
训练发散 理想的分类器应当是除了真实标签的概率为1,其余标签概率均为 0,这样计算得到其损失函数为 -ln(1) = 0 损失函数越大,说明该分类器在真实标签上分类概率越小,性能也就越差。一个非常差的分类器,可能在真实标签上的匪类概率接近于0,那么损失函数就接近于正无穷,我们成为训练发散,需要调小学习速率。 6.9 高原反应 在 ImageNet-1000 分类问题中,初始状态为均匀分布,每个类别
-
1 正向传播(Forward propagation) 回忆一下,给出一个输入特征$x$的时候,我们定义了$a^{[0]}=x$。然后对于层(layer)$l=1,2,3,\dots,N$,其中的$N$是网络中的层数,则有: $z^{[l]}=W^{[l]}a^{[l-1]}+b^{[l]}$ $a^{[l]}=g^{[l]}(z^{[l]})$ 在讲义中都是假设了非线性特征$g^{[l]}$对除
-
在使用relu激活功能时,我在实现backprop时遇到问题。我的模型有两个隐藏层,两个隐藏层中都有10个节点,输出层中有一个节点(因此有3个权重,3个偏差)。我的模型不适用于这个断开的backward\u prop函数。但是,该函数使用sigmoid激活函数(作为注释包含在函数中)与backprop一起工作。因此,我认为我把relu推导搞砸了。 谁能把我推向正确的方向?

