Certigrad 是一个概念证明,它是一种开发机器学习系统的新方法,其中包含以下组件:
应用本身
基础数学库
应用在数学上所需求的形式化描述
应用满足其形式化描述的机器可测证明
具体地说,Certigrad 是一个优化随机计算图的系统,研究人员使用 Lean Theorem Prover 对其进行了系统性的除错,它最终在底层数学上被证明是正确的。
背景:随机计算图
随机计算图通过允许节点代表随机变量,和定义损失函数为叶子结点在全图中随机选择的预测值之和,扩展了 TensorFlow 和 Theano 这些系统的计算图。Certigrad 允许用户从该项目提供的基元中构建随机计算图。创造这一系统的主要目的是找到一个能够描述随机计算图,并运行随机算法(随机反向传播)的程序。同时期望对参数损失函数梯度进行采样。
正确性
随机反向传播
以下定理可以证明我们的随机反向传播实现是正确的:https://github.com/dselsam/certigrad/blob/master/src/certigrad/backprop_correct.lean#L13-L25
通俗地说,它表示:对于任何随机计算图,backprop 计算了张量的向量,如此,每一个向量元素都是一个随机变量,这个随机变量等同于关于此参数的图的期望损失梯度。
更通俗地说:∇ E[loss(graph)] = E[backprop(graph)]
优化验证
研究人员实现了两个随机计算图转换,一个是对图进行「重新参数化」(reparameterize),让随机变量不再直接依赖于一个参数;另一个用于整合多元各向同性高斯(multivariate isotropic Gaussian)的 KL 散度。
https://github.com/dselsam/certigrad/blob/master/src/certigrad/kl.lean#L79-L90
https://github.com/dselsam/certigrad/blob/master/src/certigrad/reparam.lean#L70-L79
验证 Certigrad 程序属性
Certigrad 还包括构建随机计算图的前端语法。这里是一个解释原生变分自编码器的示例程序:
研究人员证明了上述两个经过验证的优化的确符合原始自动编码器的顺序:
反向传播在结果模型上已被证明可以正确运行,它可以满足所有必要前提条件:
正式证明
在证明定理的过程中,Lean 构建了一个正式的证书,它可以通过一个小型独立可执行程序进行自动验证,它的可靠性是基于构建良好的元理论嵌入到 Lean 的逻辑核心中,而 Lean 的可靠性已被大量开发者所证明。
问题
尽管在证明期间研究者们使用了非常高的标准,但 Certigrad 仍然有一些不够理想的地方。
我们对其数学基础进行了公理化,而不是从基本原理的层面上进行构建。
在一些地方我们采用了浮点数,即使我们的正确性定理只适用于无限精度的实数。
为了保证性能,我们在运行时用 Eigen 调用替换原始张量运算。
系统在虚拟机中执行,该虚拟机的设计不像核心逻辑的证明检验程序那样值得信赖。
表现
能被证实的正确性原则就不需要再牺牲计算效率了:证明只需被检查一次,而且不会带来过多的运行成本和运行时间。尽管目前经过我们验证的算法缺乏很多优化措施,机器学习系统的大多数训练时间都花费在了乘法矩阵上,我们仍能够通过与矩阵运算的优化库(Eigen)进行链接来轻松达到具有竞争力的表现水平。我们在 MNIST 上使用 ADAM 训练了一个自编码变贝叶斯(AEVB)模型,发现该模型的表现和 TensorFlow 相比具有竞争力(在 CPU 上)。
使用 ADAM 在 MNIST 上训练 AEVB 的脚本:https://github.com/dselsam/certigrad/blob/master/src/certigrad/aevb/mnist.lean#L44-L66
优势
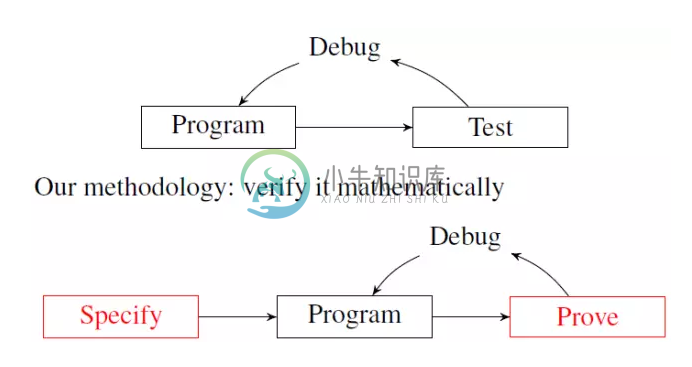
尽管新方法面临一些挑战,但它的优势是显而易见的。
调试
首先,新方法提供了一种系统性的调试机器学习系统的方法。
执行错误(Implementation errors)在机器学习系统中非常难于探测——更不用说本地化和问题解决——而且还有其他潜在的不良影响。例如;一个执行错误可能会导致不正确的梯度,让整个机器学习算法停顿,但这种情况也可能是由于训练的数据中存在噪音、错误设置、优化不合适、搜索策略不对或数值不稳定而引起的。这些其他问题是如此之常见,以至于我们通常认为任何不良行为都是由其中的一部分引起的。
因此,在实现中出现的错误如果没有被检测到,将会无限期地存在下去。而在随机系统中,错误更加难以检测,因为一些错误可能会扭曲随机变量的分布,可能需要编写定制的统计测试才能被检测出。
通过我们的方法,正式规范可以用来在逻辑层面上对机器学习系统进行彻底的测试与调试,完全不需要进行经验主义的测试。而证明规范的过程将揭示所有实现错误,疏忽和隐含假设。一旦得到证实,每个利益相关方都可以确定实现是正确的,而无需依赖于任何有关人员,或去了解程序是如何运行的。
合成
第二,我们的方法可以让一些实现的工作半自动地完成。
而使用现在的方法,编译器完全无法知晓自己需要做什么——它们只能捕捉语法错误,而新方法可以用定理推出程序需要做什么,并提供更多有意义的帮助。举一个简单的例子,假设我们需要将双层 MLP 编译成一个单原始运行器,避免图处理时需要消耗的计算资源。通常这需要包括手工打造的梯度函数。但在新方法中,定理证明器知道如何使用数学方法,包括相关的梯度规则和张量的代数性质,它可以帮助推导出新算子的梯度。
合成的可能性不仅仅是简单的自动化代数推导。在开发 Certigrad 时,研究人员证明了系统中所有复杂部位的可实现性,并使用这一过程所产生的证明义务来帮助确定程序需要做什么。正式规范最终是机器可检验的正确性证明,它使得我们能够正确地实现系统,而无需对「为什么系统正确」采取一致的全局理解。同样,大多数这样的负担被留给了电脑。
侵略性最优化(Aggressive optimizations)
第三,我们的方法可以使得稳定自动化更主动地进行转换。例如,我们可以编写一个程序来搜索随机计算图的构建元素,这样就能用分析方法进行整合,因此可以充分利用积分恒等式的大型库,和很难由手动进行模拟的程序方法。这样的过程可能在许多模型上实现超人为方差缩减,但可靠的实现会极其困难。如果该过程能为给定转换生成机器可测的数字证书,那么转换是可信的,且无需考虑过程本身的复杂性。
文档
第四,形式规范(即使没有正式的证明)也可以作为系统的精确文档,它同样可以让我们理解代码的各部分到底是在做什么、各个部分假设了什么样的先决条件和保持了怎样的不变量。这种精确的文档对于任何软件系统都是很有用的,但对于机器学习来说格外的有效,因为并不是所有的开发者都有必要的数据专业基础来填补非正式描述的鸿沟。
递增
对于高安全等级(high-assurance)系统,我们的系统已经十分节约计算资源了,但仍然需要很多的研究工作才能使其适应主流发展,因为正确性只是一个」选项「。然而,我们方法的一个关键方面可以递增地接受。我们只能在 Lean 中写一点代码,并简单的对其它部分进行打包和公理化(如同我们在 Eigen 所做的一样)。我们也可以写下来浅层的正确性属性,并只证明其中一小部分属性。我们希望随着时间的推移和工具的发展,开发者能发现进一步应用我们的方法是非常值得的。
搭建 Certigrad
Lean 还处于开发阶段,我们也更进一步地努力使得 Certigrad 可以简单地进行安装。与安装 Certigrad 特别相关的是外部功能接口(FFI)。我们复制了 Lean 项目以添加代码将 Eigen 打包入 Lean 虚拟机中,但是很快 Lean 将有一个外部功能接口,我们也就不需要重新构建 Lean 而添加到虚拟机中了。一旦 FFI 发布了,我们将把 Certigrad 移动到 Lean 的主分支下。
在那之前:
下载我们复制的 Lean(地址:https://github.com/dselsam/lean/tree/certigrad),并且按照指导手册进行构建/安装(地址:https://github.com/leanprover/lean)。
下载 Eigen 并安装它(http://bitbucket.org/eigen/eigen/get/3.3.4.tar.bz2)。
下载该仓库(Github 中的当前 repository),并在主目录下执行 leanpkg—build。
注意:构建 Certigrad 一般会话 15 分钟左右,并至少需要 7GB 的内存。
-
更多深度文章,请关注:https://yq.aliyun.com/cloud Certigrad是一种新的开源的随机计算图优化系统,它是用于开发机器学习系统的一个新途径。其中包含以下组件: 应用本身 基础数据库 应用在数学上所需求的形式化描述 应用满足其形式化描述的机器可测证明 具体来说,Certigrad是一个优化的随机计算图形系统,我们使用Lean Theorem Prover验证系统,最终证
-
给定一个随机数生成器random(7),它可以以相等的概率生成数字1,2,3,4,5,6,7(即每个数字出现的概率为1/7)。现在我们要设计一个随机数(5),它能以相等的概率(1/5)生成1,2,3,4,5。 有一种方法:每次我们随机运行(7),只有当它生成1-5时才返回。如果是6或7,再运行一次,直到它是1-5。 我有点困惑。第一个问题是: 如何用数学方法证明每个数字发生的概率是1/5?例如,假
-
1.1.1 计算机与计算 计算机是当代最伟大的发明之一。自从人类制造出第一台电子数字计算机,迄今已近 70 年。经过这么多年的发展,现在计算机已经应用到社会、生活的几乎每一个方面。人们用计 算机上网冲浪、写文章、打游戏或听歌看电影,机构用计算机管理企业、设计制造产品或从 事电子商务,大量机器被计算机控制,手机与电脑之间的差别越来越分不清,……总之计算 机似乎无处不在、无所不能。那么,计算机究竟是如
-
下面是我的函数最后的样子: 如果你想看看我在做什么,请看:http://www.sidequestsapps.com/projects/captotype/game.html
-
在这个程序中,用户必须想出一个数字,然后让计算机来猜。 2.我试过这个程序,但电脑的猜测很奇怪。计算机不会根据我的指南猜出一个数字。
-
问题内容: 我正在寻找一个随机数,并将其发布到特定user_id的数据库表中。问题是,相同的数字不能使用两次。有上百万种方法可以做到这一点,但是我希望对算法非常热衷的人能够以一种优雅的解决方案巧妙地解决问题,因为它满足以下条件: 1)最少查询数据库。2)通过内存中的数据结构进行的爬网次数最少。 本质上,这个想法是要执行以下操作 1)创建一个从0到9999999的随机数 2)检查数据库以查看该数字是
-
问题内容: 我正在尝试计算阶乘产生的数字的尾随零(这意味着数字变得很大)。以下代码采用一个数字,计算该数字的阶乘,并计算尾随零。但是,当数字大约为25!时,numZeros将不起作用。 我并不担心这段代码的效率,并且我知道有多种方法可以使这段代码的效率更好。我要弄清楚的是为什么计数大于25的数字结尾的零!不管用。 有任何想法吗? 问题答案: 您的任务不是计算阶乘,而是计算零的数量。一个好的解决方案

