Java Geometry Expert
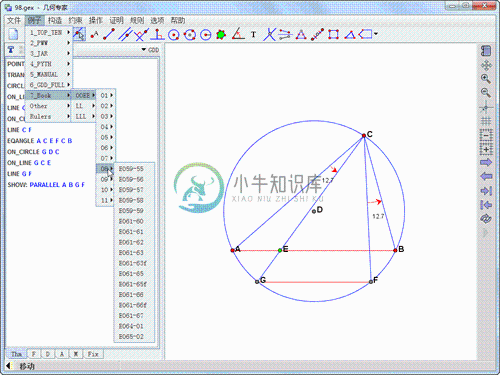
几何专家《几何专家》提供了几何动态图形变换与板块操作,可以自动证明定理,并产生简单、漂亮的证明过程,还可以自动发现几何图形的丰富性质。自从吴文俊教授七十 年代末提出几何定理自动证明的吴方法以来,中国学者在这方面的研究可谓异彩纷呈,成果累累,屡获国内外大奖。几何图形、函数图象、平面曲线、与轨迹图形, 可用于平面几何、解析几何、函数、与物理的学习与教学。作为一个定理证明器,《几何专家》使用作者的获奖研究成果,不仅可以证明大部分平面几何定理、产生 简短可读的证明,还可以自动发现几何图形的所有可能的性质、为使用者自动生成几何图形的题库。《几何专家》不仅可以帮助使用者解决难题、还可以教会使用者 解题的方法。

-
java虚拟机堆栈帧 by Berrak Nil 由Berrak Nil 在(虚拟)罐上爆炸:A帧音频入门 (Bang on A (Virtual) Can: A Primer on A-Frame Audio) A-Frame is a web framework for building virtual reality experiences. Ever since its introduct
-
问题内容: 似乎他们没有任何文档,除了在他们的官方论坛上有一些api调用之外。我有Zend框架和CodeIgniter框架的经验。OpenCart的任何高手都可以向我推荐学习它的最佳方法,并在最短的时间内对其进行掌握吗?我必须尽快做一个大项目。 问题答案: 本指南是为已经熟悉PHP,OOP和MVC架构的开发人员编写的 在下面的内容中,您将看到购物车目录侧的示例。除了在相关部分中提到的视图之外,管理
-
问题内容: 是否有适用于Java的几何库?我正在寻找解决方案以获取两个几何对象之间的交点。 问题答案: JTS是您最好的免费开源选项。您在JTS中寻找的方法在这里 至于商业选项,您可以使用ESRI的 ArcObjects库的Java JNI版本 ,该版本具有非常强大的Geometry库。ESRI库上的接口称为ITopologicalOperator 如果您要尝试做的只是几何运算,那么JTS是您的最
-
几何体组件为实体提供基本形状。这个 primitive属性定义常规形状。在计算机图形学中,几何基元是不可分的基本形状。通常还定义一个材质组件来创建完整的网孔(Mesh)。 目录 基础属性 每种几何图形类型都具有以下属性: 属性 描述 默认值 buffer 将几何体转换为BufferGeometry以减少内存使用,但代价是更难操作。 true primitive 几何体的名称(例如,下面列出的几何体
-
目标 在这一章中, 我们将学习多视图几何的基础知识。 我们将看到什么是极点,极线,极线约束等。 基本概念 当我们使用针孔相机拍摄图像时,我们会丢失一个重要的信息,即图像的深度。或者从相机的图像中的每个点有多远,因为它是3D到2D的转换。所以使用这些摄像头是否能找到深度信息是一个重要的问题。一个解决方案是使用多个相机。我们的眼睛以类似的方式使用两个相机(两只眼睛),这就是所谓的立体视觉。那么让我们来
-
在顶点和片段着色器之间有一个可选的几何着色器(Geometry Shader),几何着色器的输入是一个图元(如点或三角形)的一组顶点。几何着色器可以在顶点发送到下一着色器阶段之前对它们随意变换。然而,几何着色器最有趣的地方在于,它能够将(这一组)顶点变换为完全不同的图元,并且还能生成比原来更多的顶点。 废话不多说,我们直接先看一个几何着色器的例子: #version 330 core layout
-
[[Voronoi|泰森多边形]] - 由一组点计算Voronoi密铺或Delaunay三角剖分 。 [[Quadtree|四叉树]] - 由一组点计算四叉树。 [[Hull|赫尔]] - 由一组点计算凸包。 [[Polygon|多边形]] - 多边形计算,例如求面积、剪裁等。
-
目标 在本节中 我们将学习多视图几何的基础知识 我们将了解什么是极点,极线,极线约束等。 基础概念 当我们使用针孔相机拍摄图像时,我们失去了重要信息,即图像深度。 或者图像中的每个点距相机多远,因为它是3D到2D转换。 因此,是否能够使用这些摄像机找到深度信息是一个重要的问题。 答案是使用不止一台摄像机。 在使用两台摄像机(两只眼睛)的情况下,我们的眼睛工作方式相似,这称为立体视觉。 因此,让我们
-
在我的GEOJSON数据层中,我有一组大约20个区域。每个要素都有一个GeometryCollection,其中包含两个几何图形:一个用于定义区域的多边形和一个给出区域中心的点。 我希望多边形是不可见的,但是在地图上显示点作为标记。 此外,我希望能够根据缩放级别将区域标记设置为可见或不可见。 有没有可能只在地图上显示点,并将它们设置为可见/不可见的多边形?我知道我可以用正常的方式将它们添加到地图中

