Python决策树之基于信息增益的特征选择示例
本文实例讲述了Python决策树之基于信息增益的特征选择。分享给大家供大家参考,具体如下:
基于信息增益的特征选取是一种广泛使用在决策树(decision tree)分类算法中用到的特征选取。该特征选择的方法是通过计算每个特征值划分数据集获得信息增益,通过比较信息增益的大小选取合适的特征值。
一、定义
1.1 熵
信息的期望值,可理解为数据集的无序度,熵的值越大,表示数据越无序,公式如下:
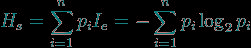
其中H表示该数据集的熵值, pi表示类别i的概率, 若所有数据集只有一个类别,那么pi=1,H=0。因此H=0为熵的最小值,表示该数据集完全有序。
1.2 信息增益
熵的减少或者是数据无序度的减少。
二、流程
1、计算原始数据的信息熵H1
2、选取一个特征,根据特征值对数据进行分类,再对每个类别分别计算信息熵,按比例求和,得出这种划分方式的信息熵H2
3、计算信息增益:
infoGain = H1 - H2
4、根据2,3计算所有特征属性对应的信息增益,保留信息增益较大的特征属性。
三、实例
海洋生物数据
| 被分类项\特征 | 不浮出水面是否可以生存 | 是否有脚蹼 | 属于鱼类 |
|---|---|---|---|
| 1 | 是 | 是 | 是 |
| 2 | 是 | 是 | 是 |
| 3 | 是 | 否 | 否 |
| 4 | 否 | 是 | 否 |
| 5 | 否 | 是 | 否 |
3.1 原始数据信息熵
p(是鱼类) = p1 =0.4
p(非鱼类) = p2 =0.6
通过信息熵公式可得原始数据信息熵 H1 = 0.97095
3.2 根据特征分类计算信息熵
选择'不服出水面是否可以生存'作为分析的特征属性
可将数据集分为[1,2,3]与[4,5],分别占0.6和0.4。
[1,2,3]可计算该类数据信息熵为 h1=0.918295834054
[4,5] 可计算该类数据信息熵为 h2=0
计算划分后的信息熵 H2 = 0.6 * h1 + 0.4 * h2 = 0.550977500433
3.3 计算信息增益
infoGain_0 = H1-H2 = 0.419973094022
3.4 特征选择
同理可得对特征'是否有脚蹼'该特征计算信息增益 infoGain_1 = 0.170950594455
比较可得,'不服出水面是否可以生存'所得的信息增益更大,因此在该实例中,该特征是最好用于划分数据集的特征
四、代码
# -*- coding:utf-8 -*- #! python2 import numpy as np from math import log data_feature_matrix = np.array([[1, 1], [1, 1], [1, 0], [0, 1], [0, 1]]) # 特征矩阵 category = ['yes', 'yes', 'no', 'no', 'no'] # 5个对象分别所属的类别 def calc_shannon_ent(category_list): """ :param category_list: 类别列表 :return: 该类别列表的熵值 """ label_count = {} # 统计数据集中每个类别的个数 num = len(category_list) # 数据集个数 for i in range(num): try: label_count[category_list[i]] += 1 except KeyError: label_count[category_list[i]] = 1 shannon_ent = 0. for k in label_count: prob = float(label_count[k]) / num shannon_ent -= prob * log(prob, 2) # 计算信息熵 return shannon_ent def split_data(feature_matrix, category_list, feature_index, value): """ 筛选出指定特征值所对应的类别列表 :param category_list: 类别列表 :param feature_matrix: 特征矩阵 :param feature_index: 指定特征索引 :param value: 指定特征属性的特征值 :return: 符合指定特征属性的特征值的类别列表 """ # feature_matrix = np.array(feature_matrix) ret_index = np.where(feature_matrix[:, feature_index] == value)[0] # 获取符合指定特征值的索引 ret_category_list = [category_list[i] for i in ret_index] # 根据索引取得指定的所属类别,构建为列表 return ret_category_list def choose_best_feature(feature_matrix, category_list): """ 根据信息增益获取最优特征 :param feature_matrix: 特征矩阵 :param category_list: 类别列表 :return: 最优特征对应的索引 """ feature_num = len(feature_matrix[0]) # 特征个数 data_num = len(category_list) # 数据集的个数 base_shannon_ent = calc_shannon_ent(category_list=category_list) # 原始数据的信息熵 best_info_gain = 0 # 最优信息增益 best_feature_index = -1 # 最优特征对应的索引 for f in range(feature_num): uni_value_list = set(feature_matrix[:, f]) # 该特征属性所包含的特征值 new_shannon_ent = 0. for value in uni_value_list: sub_cate_list = split_data(feature_matrix=feature_matrix, category_list=category_list, feature_index=f, value=value) prob = float(len(sub_cate_list)) / data_num new_shannon_ent += prob * calc_shannon_ent(sub_cate_list) info_gain = base_shannon_ent - new_shannon_ent # 信息增益 print '初始信息熵为:', base_shannon_ent, '按照特征%i分类后的信息熵为:' % f, new_shannon_ent, '信息增益为:', info_gain if info_gain > best_info_gain: best_info_gain = info_gain best_feature_index = f return best_feature_index if __name__ == '__main__': best_feature = choose_best_feature(data_feature_matrix, category) print '最好用于划分数据集的特征为:', best_feature
运行结果:
初始信息熵为: 0.970950594455 按照特征0分类后的信息熵为: 0.550977500433 信息增益为: 0.419973094022
初始信息熵为: 0.970950594455 按照特征1分类后的信息熵为: 0.8 信息增益为: 0.170950594455
最好用于划分数据集的特征为: 0
更多关于Python相关内容感兴趣的读者可查看本站专题:《Python数学运算技巧总结》、《Python数据结构与算法教程》、《Python函数使用技巧总结》、《Python字符串操作技巧汇总》、《Python入门与进阶经典教程》及《Python文件与目录操作技巧汇总》
希望本文所述对大家Python程序设计有所帮助。
-
本文向大家介绍信息增益相关面试题,主要包含被问及信息增益时的应答技巧和注意事项,需要的朋友参考一下 特征A对训练数据集D的信息增益g(D,A) = H(D) - H(D|A) 由于特征A而使得对数据集D的分类的不确定性减少的程度。信息增益大的特征具有更强的分类能力。
-
本文向大家介绍基于Python实现的ID3决策树功能示例,包括了基于Python实现的ID3决策树功能示例的使用技巧和注意事项,需要的朋友参考一下 本文实例讲述了基于Python实现的ID3决策树功能。分享给大家供大家参考,具体如下: ID3算法是决策树的一种,它是基于奥卡姆剃刀原理的,即用尽量用较少的东西做更多的事。ID3算法,即Iterative Dichotomiser 3,迭代二叉树3代,
-
本文向大家介绍python基于ID3思想的决策树,包括了python基于ID3思想的决策树的使用技巧和注意事项,需要的朋友参考一下 这是一个判断海洋生物数据是否是鱼类而构建的基于ID3思想的决策树,供大家参考,具体内容如下 最后我们测试一下这个脚本即可,如果想把这个生成的决策树用图像画出来,也只是在需要在脚本里面定义一个plottree的函数即可。 以上就是本文的全部内容,希望对大家的学习有所帮助
-
特征选择在于选取对训练集有分类能力的特征,这样可以提高决策树学习的效率。 通常特征选择的准则是信息增益或信息增益比。 信息增益 信息增益(information gain)表示得知特征$$X$$的信息而使得类$$Y$$的信息不确定性减少称。 特征$$A$$对训练数据集$$D$$的信息增益$$g(D,A)$$,定义为集合$$D$$的经验熵$$H(D)$$与特征$$A$$在给定条件下$$D$$的经验条
-
主要内容:纯度的概念,纯度度量规则,纯度度量方法首先来看一个“我想你来猜”的游戏,游戏规则很简单:一个人从脑海中构建一个事物,另外几个人最多可以向他提问 20 个问题,游戏规定,问题的答案只能用是或者否来回答。问问题的人通过回答者的“答案”来推分析、逐步缩小待猜测事物的范围,从而来判断他想的是什么。其实这个游戏与决策树工作过程相似。 那么你有没有考虑过要怎样选择“问什么问题”呢,在这里“问什么问题”就相当于决策树算法中的“判别条件”。选择什么判
-
RFormula通过一个R model formula选择一个特定的列。 目前我们支持R算子的一个受限的子集,包括~,.,:,+,-。这些基本的算子是: ~ 分开target和terms + 连接term,+ 0表示删除截距(intercept) - 删除term,- 1表示删除截距 : 交集 . 除了target之外的所有列 假设a和b是double列,我们用下面简单的例子来证明RFor

