Python数据可视化正态分布简单分析及实现代码

Python说来简单也简单，但是也不简单，尤其是再跟高数结合起来的时候。。。

正态分布（Normaldistribution），也称“常态分布”，又名高斯分布（Gaussiandistribution），最早由A.棣莫弗在求二项分布的渐近公式中得到。C.F.高斯在研究测量误差时从另一个角度导出了它。P.S.拉普拉斯和高斯研究了它的性质。是一个在数学、物理及工程等领域都非常重要的概率分布，在统计学的许多方面有着重大的影响力。

正态曲线呈钟型，两头低，中间高，左右对称因其曲线呈钟形，因此人们又经常称之为钟形曲线。

若随机变量X服从一个数学期望为μ、方差为σ^2的正态分布，记为

N(μ，σ^2)

其概率密度函数为正态分布的期望值μ决定了其位置，其标准差σ决定了分布的幅度。当μ=0,σ=1时的正态分布是标准正态分布。其概率密度函数为：

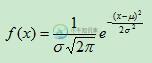
我们通常所说的标准正态分布是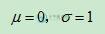的正态分布：

概率密度函数

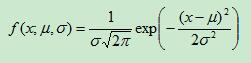
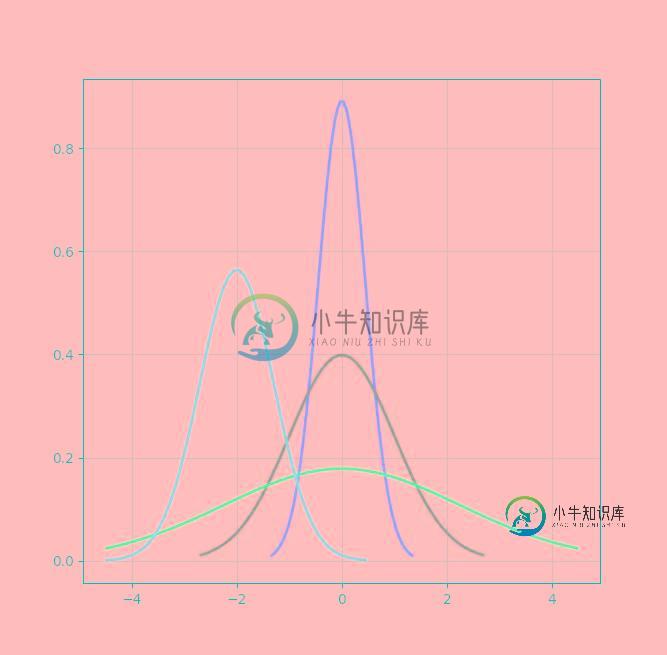
代码实现：

 # Python实现正态分布
 # 绘制正态分布概率密度函数
 u = 0 # 均值μ
 u01 = -2
 sig = math.sqrt(0.2) # 标准差δ
 sig01 = math.sqrt(1)
 sig02 = math.sqrt(5)
 sig_u01 = math.sqrt(0.5)
 x = np.linspace(u - 3*sig, u + 3*sig, 50)
 x_01 = np.linspace(u - 6 * sig, u + 6 * sig, 50)
 x_02 = np.linspace(u - 10 * sig, u + 10 * sig, 50)
 x_u01 = np.linspace(u - 10 * sig, u + 1 * sig, 50)
 y_sig = np.exp(-(x - u) ** 2 /(2* sig **2))/(math.sqrt(2*math.pi)*sig)
 y_sig01 = np.exp(-(x_01 - u) ** 2 /(2* sig01 **2))/(math.sqrt(2*math.pi)*sig01)
 y_sig02 = np.exp(-(x_02 - u) ** 2 / (2 * sig02 ** 2)) / (math.sqrt(2 * math.pi) * sig02)
 y_sig_u01 = np.exp(-(x_u01 - u01) ** 2 / (2 * sig_u01 ** 2)) / (math.sqrt(2 * math.pi) * sig_u01)
 plt.plot(x, y_sig, "r-", linewidth=2)
 plt.plot(x_01, y_sig01, "g-", linewidth=2)
 plt.plot(x_02, y_sig02, "b-", linewidth=2)
 plt.plot(x_u01, y_sig_u01, "m-", linewidth=2)
 # plt.plot(x, y, 'r-', x, y, 'go', linewidth=2,markersize=8)
 plt.grid(True)
 plt.show()

总结

以上就是本文关于Python数据可视化正态分布简单分析及实现代码的全部内容，希望对大家有所帮助。感兴趣的朋友可以继续参阅本站其他Python和算法相关专题，如有不足之处，欢迎留言指出。感谢朋友们对本站的支持！