Java语言实现非递归实现树的前中后序遍历总结

前言

三种遍历的递归写法都很好写，所以总结一下非递归写法。

先贴一张图复习一下三种遍历方式就进入正文啦~

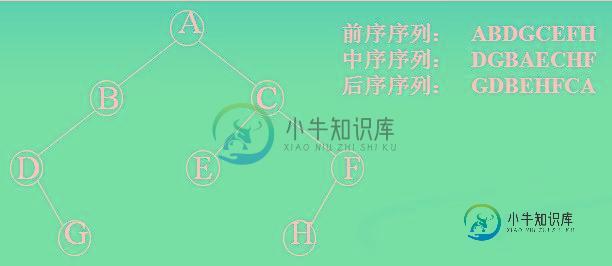
【注：本文所有代码实现中树的结点定义如下：

public class Node {
  int val;
  Node left;
  Node right;
  Node parent;
  Node() {}
  Node(int val) {
    this.val = val;
  }
}

1.前序遍历

实现思路：

前序遍历的顺序是：根结点 -> 左孩子 -> 右孩子

借助一个栈结构先将根结点压入栈，然后循环每次取出栈顶元素，直到栈为空。如果当前结点有右孩子就先将右孩子压入栈中，如果当前结点有左孩子就将左孩子压入栈中，这里注意顺序，因为栈的结构是先进后出的，为了保证先遍历到左孩子就应该后压左孩子~

代码实现：

【代码使用直接输出的方式打印中序遍历结果，也可以放入一个list中存储~】

public void preOrder(Node head) {
    System.out.println("pre-order:");
    if(head != null) {
      Stack<Node> stack = new Stack<>();
      stack.push(head);
      while(!stack.isEmpty()) {
        head = stack.pop();
        System.out.print(head.val + " ");
        if (head.right != null)
          stack.push(head.right);
        if (head.left != null)
          stack.push(head.left);
      }
    }
  }

2.中序遍历

实现思路：

中序遍历的顺序：左孩子 -> 根结点 -> 右孩子

借助栈结构，将当前结点的左孩子依次入栈直到没有左孩子了就弹出栈顶元素并打印，如果弹出的结点有右孩子就将右孩子的左边界依次入栈，循环…

比如文章开始的那个图中，先将A，B，D依次入栈，此时栈顶元素是D，弹出并打印，D结点有右孩子，将D的右孩子的左边界依次入栈，压入结点G，结点G没有左孩子所以弹出并打印G，此时栈顶元素是B，循环…直到栈中为空且当前结点为空时遍历结束。

代码实现：

public static void inOrderTraverse(Node head) {
    System.out.println("in-order:");
    if(head != null) {
      Stack<Node> stack = new Stack<>();
      while(!stack.isEmpty() || head != null) {
        if(head != null) {
          // 当前节点不为空, 将自己压进栈并将自己的左孩子作为当前节点（压入左边界）
          stack.push(head);
          head = head.left;
        }else {
          // 当前节点为空（没有左孩子了）, 将栈顶元素弹出作为当前节点, 并将当前节点的右孩子压进栈
          head = stack.pop();
          System.out.print(head.val + " ");
          head = head.right;
        }
      }
    }
  }

3.后序遍历

实现思路：

后序遍历的顺序：左孩子 -> 右孩子 -> 根结点

仔细想一下，打印每个结点需要访问根结点三次，先从根结点开始找到左孩子，返回再找到右孩子，再返回到根结点，需要访问根结点三次，直接按照当前顺序进行遍历不知如何下手，那么我们可以换一个角度去考虑。

栈结构是先进后出的，那我们不妨借助一个栈先存储 根结点 -> 右孩子 -> 左孩子 的结果，再将其依次弹出就是后序遍历的顺序了。

那实现 根结点 -> 右孩子 -> 左孩子 的方法就很简单了，回忆一下刚才说的前序遍历的方式，前序遍历是先要左孩子，就后压入左孩子，反之，将前序遍历的逻辑改写为：弹出每个栈顶结点作为当前结点并存储到一个辅助栈中，如果当前结点有左孩子就先压入左孩子，如果有右孩子就后压入右孩子，每次取栈顶弹出到辅助栈中。最后将得到的辅助栈中元素依次弹出得到的就是后序遍历的结果。

代码实现：

public static void posOrderTraverse(Node head) {
    System.out.println("pos-order");
    if(head != null) {
      Stack<Node> stack1 = new Stack<>();
      Stack<Node> stack2 = new Stack<>();   // 辅助栈，存储 根 -> 右 -> 左 的结果
      stack1.push(head);
      while(!stack1.isEmpty()) {
        head = stack1.pop();
        stack2.push(head);
        // 有左孩子就先压入左孩子
        if(head.left != null)
          stack1.push(head.left);
        // 有右孩子就后压入右孩子
        if(head.right != null)
          stack1.push(head.right);
      }
      // 逆序打印 根 -> 右 -> 左 的结果，就是后序遍历的结果
      while(!stack2.isEmpty())
        System.out.print(stack2.pop().val + " ");
    }
  }

总结

以上就是这篇文章的全部内容了，希望本文的内容对大家的学习或者工作具有一定的参考学习价值，谢谢大家对小牛知识库的支持。如果你想了解更多相关内容请查看下面相关链接