《二叉树》专题
-
如何为二叉搜索树编写test LeavesCorrectWhentreIsPerfect()
我实现了一个二进制搜索树,并为它编写了一个测试类(在JUNIT测试中)。除了一次考试,所有的考试都通过了。当我调试代码时,测试leavesIsTrue tWhenTreeIs完美()会得到一条消息。 预期: 请记住,所有其他测试都会通过,我不认为这是树代码的问题。 你如何理解测试的描述? 测试等级:
-
访问二叉搜索树的外部节点
在“二叉树”中,一个外部节点是一个没有任何子节点的节点,无论是左的还是右的,如果我错了,请纠正我-在“二叉树”中,一个外部节点总是空的,因为根据我的课堂讲稿,一个内部节点总是有两个子节点,即使没有创建,但我们假设该内部节点的子节点是空的。那么,如果外部节点为空,我如何访问它呢? 我将这段代码作为BST节点类的一部分编写: Last方法给我nullPointerException
-
二叉搜索树序迭代器next方法
-
在二叉查找树中实现nodeCount()和folCount()
我正在尝试将leafCount()和nodeCount()实现到这个递归二叉树程序中。在测试时,这两种方法(或它们的测试)都会失败,因此显然它们没有按预期工作。我搞不清自己哪里做错了,哪里想错了。如果有人能解释我做错了什么或指出问题所在,我将非常感激。
-
使用java插入二叉树不起作用
我目前正在学习使用java的树,在二叉树中插入项时出现了一些错误,我不知道为什么它不起作用 这是代码:树节点: 树类: 每当我添加一个项目,根仍然为空,没有右或左的项目,如果有人能帮助我,我会非常感激
-
在非二叉树中查找子级(递归)
我有TreeNode类——非二叉树(
-
带有键和值的Python二叉搜索树
我需要实现一个Binary Search Tree类作为家庭作业,但我很难实现insert函数。我在谷歌搜索了很多,想找到一些解决方案或可能的方法,但他们都没有使用过键和值(大多只是值),或者如果他们也使用了键,他们有很多单独的功能,我想这是不允许的。 因此,预构建的只是: 现在的问题是,如果我想检查例如值是否小于或大于当前节点以将其放在右侧或左侧,我会收到诸如“root未定义”或“root.ri
-
如何在python中打印二叉搜索树?
下面是一个二叉查找树,它有一个根节点、一个左节点和一个右节点。代码有效,但我想显示这个二叉查找树,这样我就可以看到图层中的每个节点…这是代码…
-
第 26 章 链表、二叉树和哈希表
第 26 章 链表、二叉树和哈希表 目录 1. 链表 1.1. 单链表 1.2. 双向链表 1.3. 静态链表 1.4. 本节综合练习 2. 二叉树 2.1. 二叉树的基本概念 2.2. 排序二叉树 3. 哈希表
-
【LeetCode】124 二叉树中的最大路径和
这道题是 LeetCode 124 题。 给定一个非空二叉树,返回其最大路径和。注意,这里的“路径”并非自顶向下的单向路径,而是二叉树中任意连通的路径,可以在任一节点开始和结束。比如对于下图的二叉树,10->12->9 是一个最大路径: -9 / \ 1 12 / \ 10 9 分析 首先定义“端点”的概念。一条路径有两个端点:起点和终点。比如上述示例中,
-
为什么二进制堆必须是一棵完整的二叉树?
堆属性说: 如果A是B的父节点,则节点A的键相对于节点B的键进行排序,并在堆中应用相同的排序。要么父节点的键总是大于或等于子节点的键,最高键在根节点(这种堆称为最大堆),要么父节点的键小于或等于子节点的键,最低键在根节点(最小堆)。 但是为什么在这个wiki中,二进制堆必须是一个完整的二叉树呢?在我的印象中,堆属性并不意味着这一点。
-
JS二叉树的简单实现方法示例
本文向大家介绍JS二叉树的简单实现方法示例,包括了JS二叉树的简单实现方法示例的使用技巧和注意事项,需要的朋友参考一下 本文实例讲述了JS二叉树的简单实现方法。分享给大家供大家参考,具体如下: 今天学习了一下 二叉树的实现,在此记录一下 简单的二叉树实现,并且实现升序和降序排序输出 更多关于JavaScript相关内容感兴趣的读者可查看本站专题:《JavaScript数据结构与算法技巧总结》、《J
-
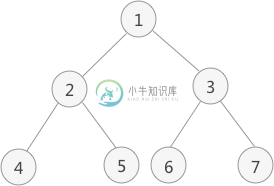 二叉树后序遍历(递归与非递归)
二叉树后序遍历(递归与非递归)主要内容:递归实现,非递归实现二叉树后序遍历的实现思想是:从根节点出发,依次遍历各节点的左右子树,直到当前节点左右子树遍历完成后,才访问该节点元素。 图 1 二叉树 如图 1 中,对此二叉树进行后序遍历的操作过程为: 从根节点 1 开始,遍历该节点的左子树(以节点 2 为根节点); 遍历节点 2 的左子树(以节点 4 为根节点); 由于节点 4 既没有左子树,也没有右子树,此时访问该节点中的元素 4,并回退到节点 2 ,遍
-
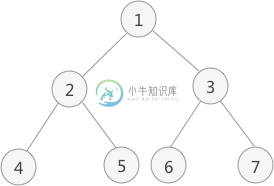 二叉树中序遍历(递归和非递归)
二叉树中序遍历(递归和非递归)主要内容:递归实现,非递归实现二叉树中序遍历的实现思想是: 访问当前节点的左子树; 访问根节点; 访问当前节点的右子树; 图 1 二叉树 以图 1 为例,采用中序遍历的思想遍历该二叉树的过程为: 访问该二叉树的根节点,找到 1; 遍历节点 1 的左子树,找到节点 2; 遍历节点 2 的左子树,找到节点 4; 由于节点 4 无左孩子,因此找到节点 4,并遍历节点 4 的右子树; 由于节点 4 无右子树,因此节点 2 的左子
-
 二叉树先序遍历(递归与非递归)
二叉树先序遍历(递归与非递归)主要内容:递归实现,非递归实现二叉树先序遍历的实现思想是: 访问根节点; 访问当前节点的左子树; 若当前节点无左子树,则访问当前节点的右子树; 图 1 二叉树 以图 1 为例,采用先序遍历的思想遍历该二叉树的过程为: 访问该二叉树的根节点,找到 1; 访问节点 1 的左子树,找到节点 2; 访问节点 2 的左子树,找到节点 4; 由于访问节点 4 左子树失败,且也没有右子树,因此以节点 4 为根节点的子树遍历完成。但节点
