《推荐算法工程师》专题
-
java实现最短路径算法之Dijkstra算法本文向大家介绍java实现最短路径算法之Dijkstra算法，包括了java实现最短路径算法之Dijkstra算法的使用技巧和注意事项，需要的朋友参考一下 前言 Dijkstra算法是最短路径算法中为人熟知的一种，是单起点全路径算法。该算法被称为是“贪心算法”的成功典范。本文接下来将尝试以最通俗的语言来介绍这个伟大的算法，并赋予java实现代码。 一、知识准备： 1、表示图的数据结构 用于存储图的
-
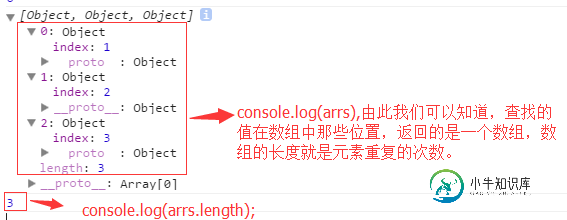
javascript数据结构与算法之检索算法本文向大家介绍javascript数据结构与算法之检索算法，包括了javascript数据结构与算法之检索算法的使用技巧和注意事项，需要的朋友参考一下 查找数据有2种方式，顺序查找和二分查找。顺序查找适用于元素随机排列的列表。二分查找适用于元素已排序的列表。二分查找效率更高，但是必须是已经排好序的列表元素集合。 一：顺序查找 顺序查找是从列表的第一个元素开始对列表元素逐个进行判断，直到找到了想要的
-
无法计算出此算法的运行时间
我被要求为这个问题编写一个算法：给我们一个数组A，我们想知道数组中是否有两个元素U和L，U和L=K 我是这样写我的算法的: 但问题是，这个算法的运行时间是多少？它是O（nlogn）吗？如果是，为什么？如果不是，我如何在O（nlogn）中实现它？
-
数据结构与算法 - 最短路径算法
Dijkstra——贪心算法 从一个顶点到其余顶点的最短路径 设G=(V,E)是一个带权有向图，把图中顶点集合V分成两组，第1组为已求出最短路径的顶点（用S表示，初始时S只有一个源点，以后每求得一条最短路径v,...k，就将k加到集合S中，直到全部顶点都加入S）。第2组为其余未确定最短路径的顶点集合（用U表示），按最短路径长度的递增次序把第2组的顶点加入S中。 步骤： 1. 初始时，S只包含源点，
-
js判断变量初始化的三种形式及推荐用的形式
本文向大家介绍js判断变量初始化的三种形式及推荐用的形式，包括了js判断变量初始化的三种形式及推荐用的形式的使用技巧和注意事项，需要的朋友参考一下
-
DropDownList 下拉框选择改变促发事件和防全局刷新(推荐)
本文向大家介绍DropDownList 下拉框选择改变促发事件和防全局刷新(推荐)，包括了DropDownList 下拉框选择改变促发事件和防全局刷新(推荐)的使用技巧和注意事项，需要的朋友参考一下 代码： asp:ScriptManager 概述： 1, ScriptManager(脚本控制器)是asp.net ajax存在的基础. 2, 一个页面只允许有一个ScriptManager,并且放在
-
不推荐使用Objective-C选择器的字符串文字；改用“#selector”[duplicate]
我有以下代码： 在运行应用程序时，当错误修复工作发生另一个错误时，就会出现此错误
-
SparseBooleanArray的明确目的是什么？[我为此推荐了官方android网站]
问题内容： 我为“ SparseBooleanArray”类引用了android文档站点，但仍不知道该类的目的是什么？为了什么目的，我们需要使用该类？ 这是文档链接 http://developer.android.com/reference/android/util/SparseBooleanArray.html 问题答案： 根据我从文档中得到的信息，它是将Integer值映射到布尔值的。 也就
-
由于不推荐使用MSSQL，如何使SQLSRV扩展与PHP一起使用？
问题内容： 我升级到PHP5.3，并注意到缺少php_mssql.dll。稍作查询后，似乎5.3放弃了对mssql的支持。因此，我从Microsoft下载了驱动程序，但似乎无法正常运行。 我在窗户上。将文件解压缩到PHP 5.3的ext目录中后，该怎么办？ 问题答案： 引用http://php.net/manual/en/intro.mssql.php： MSSQL扩展名在带有PHP 5.3或更高
-
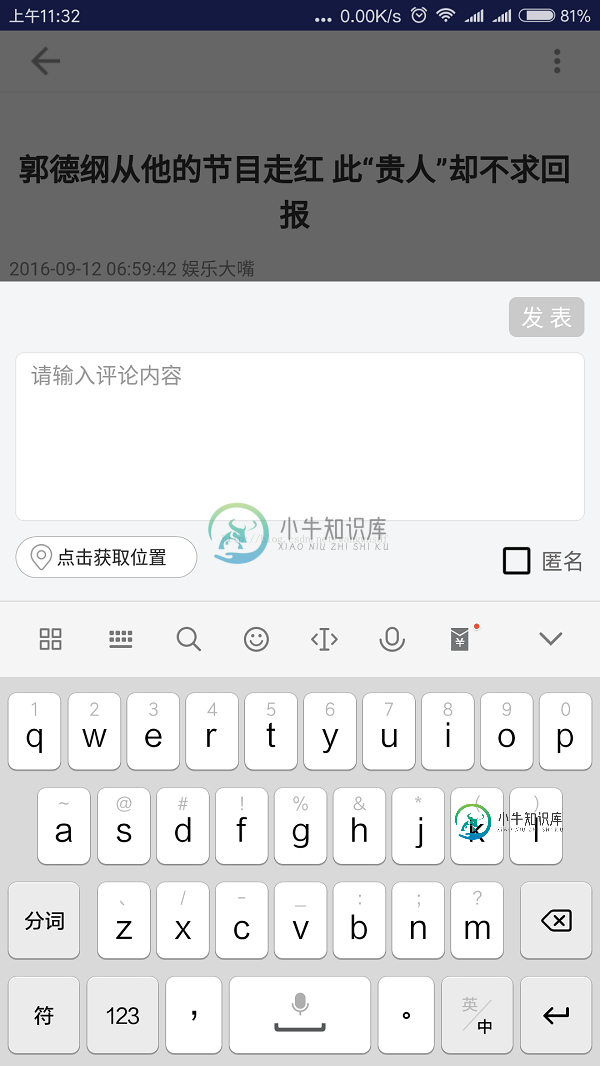
Android 仿今日头条评论时键盘自动弹出的效果(推荐)本文向大家介绍Android 仿今日头条评论时键盘自动弹出的效果(推荐)，包括了Android 仿今日头条评论时键盘自动弹出的效果(推荐)的使用技巧和注意事项，需要的朋友参考一下 Android 仿今日头条评论时键盘自动弹出的效果：当点击评论时，弹出对话框，同时弹出软键盘，当点击返回键时，将对话框关闭，不只是关闭软键盘。 效果图： 对这个对话框设置一个style效果： 并设置Dialog的监听返回
-
Spring boot中使用Spring-data-jpa方便快捷的访问数据库(推荐)
本文向大家介绍Spring boot中使用Spring-data-jpa方便快捷的访问数据库(推荐)，包括了Spring boot中使用Spring-data-jpa方便快捷的访问数据库(推荐)的使用技巧和注意事项，需要的朋友参考一下 什么是JPA JPA(Java Persistence API)是Sun官方提出的Java持久化规范。它为Java开发人员提供了一种对象/关联映射工具来管理Java
-
Dubbo推荐使用什么序列化框架，你知道的还有哪些？
本文向大家介绍Dubbo推荐使用什么序列化框架，你知道的还有哪些？相关面试题，主要包含被问及Dubbo推荐使用什么序列化框架，你知道的还有哪些？时的应答技巧和注意事项，需要的朋友参考一下 推荐使用Hessian序列化，还有Duddo、FastJson、Java自带序列化。
-
你能推荐我在控制器服务中使用的泛型名称吗？
服务 控制器
-
.loc、.iloc和不推荐使用的.ix的速度。为什么不使用.ix？
关于堆栈溢出，有多个问题比较loc、iloc和ix，比如这一个，还有多个问题讨论速度差异，比如这一个。似乎大家的共识是.ix速度更快，但它已被弃用。 这就引出了我的问题，如果. ix更快，尤其是在基于标签的索引中，为什么要弃用它？为什么你不想使用更快的方法？我发现弃用. ix的唯一原因是它混淆了人们，因为它对标签和整数都有效。我是不是漏了什么？或者. ix的唯一缺点是它令人困惑，因此将来可能不支持
-
不推荐支持遗留功能；您正在发送“deviceName”，该功能无效
我试图用Java和Appium建立一个项目。事情是，我只是在学习，我被困在问题的前几行代码截图上 我正在尝试设置“所需功能”，但有一个问题表明这些功能无效。我也尝试查看文档，但无法弄清楚如何修复它。如果有人能帮忙，那将是很大的帮助。