《推荐算法实习》专题

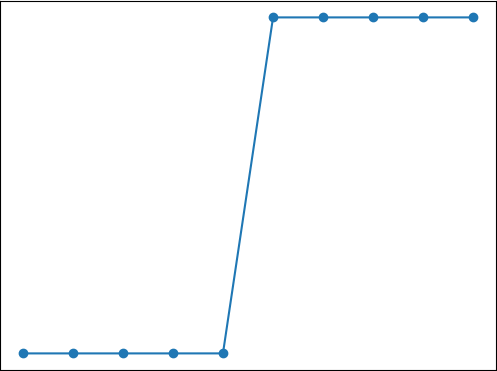
主要内容：什么是分类问题？,Logistic回归算法我们知道有监督学习分为“回归问题”和“分类问题”，前面我们已经认识了什么是“回归问题”，从本节开始我们将讲解“分类问题”的相关算法。在介绍具体的算法前，我们先聊聊到底什么是分类问题。 什么是分类问题？ 其实想要理解“分类”问题非常的简单，我们不妨拿最简单的“垃圾分类处理”的过程来认识一下这个词。现在考虑以下场景： 小明拎着两个垃圾袋出门倒垃圾，等走到垃圾回收站的时候，小明发现摆放着两个垃圾桶，上面

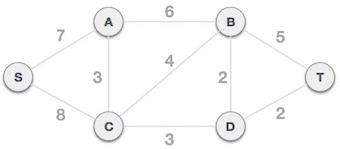
主要内容：普里姆算法的具体实现了解了什么是 最小生成树后，本节为您讲解如何用普里姆（prim）算法查找连通网（带权的连通图）中的最小生成树。 普里姆算法查找最小生成树的过程，采用了贪心算法的思想。对于包含 N 个顶点的连通网，普里姆算法每次从连通网中找出一个权值最小的边，这样的操作重复 N-1 次，由 N-1 条权值最小的边组成的生成树就是最小生成树。 那么，如何找出 N-1 条权值最小的边呢？普里姆算法的实现思路是： 将连通

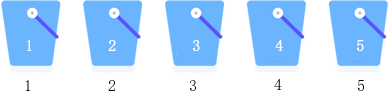
主要内容：桶排序算法的实现思路,桶排序算法的具体实现桶排序（又称箱排序）是一种基于分治思想、效率很高的排序算法，理想情况下对应的时间复杂度为 O(n)。 接下来，我们系统地学习一下桶排序算法。 桶排序算法的实现思路 假设一种场景，对 {5, 2, 1, 4, 3} 进行升序排序，桶排序算法的实现思路是： 准备 5 个桶，从 1~5 对它们进行编号； 将待排序序列的各个元素放置到相同编号的桶中； 从 1 号桶开始，依次获取桶中放置的元素，得到的就是一

主要内容：算法是什么,伪代码描述算法要想成为一名合格的程序员，除了至少掌握一门编程语言，更重要的是多动手实践，积累足够的代码量，提升自己“遇到问题，解决问题”的能力。任何一门编程语言的学习，本质就是学习它规定的语法，整个过程只能死记硬背，几乎没有捷径。但是，提高“解决问题”的能力是有捷径可寻的，比如掌握一些算法。 提到“算法”，很多人都觉得它高深莫测、晦涩难懂。事实上的确存在一些算法，学员必须具备优秀的数学基础和编程能力才能驾驭。但

程序调用自身的编程技巧称为递归（recursion），它做为一种算法在程序设计语言中广泛应用。 Java 支持递归，在 Java 编程中，递归是允许方法调用自身调用的属性。调用自身的方法称为是递归的。 递归的典型例子是数字的阶乘。数字 N 的阶乘是 1 到 N 之间所有整数的乘积。例如 3 的阶乘就是 1×2×3。下面的程序使用递归来计算数字的阶乘。 该程序产生的输出如下所示： 3的阶乘是 6 4

我正试图为一个双人8×8棋盘游戏创造一个人工智能对手。经过研究，我发现极大极小算法足够方便地完成这项工作。我创造的人工智能对手将与另一个人工智能对手或人类对战。 我对理解最小最大值算法有疑问。 我试图只创建一个AI对手，但在网络上找到的解释说我需要为两个玩家（最小玩家和最大玩家）编写代码，正如我从下面的伪代码中了解的那样。 我可以进一步理解，最大玩家将是我将要开发的AI，最小玩家是对手。 我的问题

我正在使用来调度多个java作业。我想知道在以下情况下会发生什么： 如果我在使用， 运行命令，长首字母延迟，长周期，时间单位 用于调度5个线程池大小为1的作业 p1-5（以分钟为单位的执行间隔） p2-5 p3-5 p4-7 p5-10 5分钟后，p1、p2和p3将激活争用。 将作业分配给一个可用线程使用什么算法？他们会以循环方式分配吗？ 现在在第7分钟，假设p1和p2完成，p4变为活动状态，但p

主要内容：Nelder–Mead单纯形算法,　最小二乘,求根包提供了几种常用的优化算法。 该模块包含以下几个方面 - 使用各种算法(例如BFGS，Nelder-Mead单纯形，牛顿共轭梯度，COBYLA或SLSQP)的无约束和约束最小化多元标量函数() 全局(蛮力)优化程序(例如，，) 最小二乘最小化()和曲线拟合()算法 标量单变量函数最小化()和根查找() 使用多种算法(例如，Powell，Levenberg-Marquardt混合或Newton-Kr

先来先服务(FCFS, First Come First Serve) 短作业优先(SJF, Shortest Job First) 最高优先权调度(Priority Scheduling) 时间片轮转(RR, Round Robin) 多级反馈队列调度(multilevel feedback queue scheduling) 常见的调度算法总结:http://www.jianshu.com/p

前言 算法主要包括： 1、排序 排序一定要准备。 2、堆栈、队列、链表 队列和链表可以不准备，但是堆栈一定要准备。 一个小技巧：JS的数组本身就具备堆栈和队列的特性。比如：top、push、shift、unshift这四个api，本身就帮我们实现了堆栈和队列。 堆栈：先进后出。 3、递归 递归是一定不能偷懒的。算法比较难的时候，一般要用到递归。 4、波兰式和逆波兰式 总结： 比如阿里，如果基础题答

  梯度下降（GD）是最小化风险函数、损失函数的一种常用方法，随机梯度下降和批量梯度下降是两种迭代求解思路。 1 批量梯度下降算法   假设h(theta)是要拟合的函数，J(theta)是损失函数，这里theta是要迭代求解的值。这两个函数的公式如下,其中m是训练集的记录条数，j是参数的个数：   梯度下降法目的就是求出使损失函数最小时的theta。批量梯度下降的求解思路如下： 对损失函数求th

前言 初级实现 1. 链表实现无序符号表 2. 二分查找实现有序符号表 二叉查找树 1. get() 2. put() 3. 分析 4. floor() 5. rank() 6. min() 7. deleteMin() 8. delete() 9. keys() 10. 分析 2-3 查找树 1. 插入操作 2. 性质 红黑树 1. 左旋转 2. 右旋转 3. 颜色转换 4. 插入 5. 分析

算法分析 排序 并查集 栈和队列 符号表 其它 参考资料 Sedgewick, Robert, and Kevin Wayne. Algorithms. Addison-Wesley Professional, 2011.

前言 Quick Find Quick Union 加权 Quick Union 路径压缩的加权 Quick Union 比较 前言 用于解决动态连通性问题，能动态连接两个点，并且判断两个点是否连通。 方法 描述 UF(int N) 构造一个大小为 N 的并查集 void union(int p, int q) 连接 p 和 q 节点 int find(int p) 查找 p 所在的连通分量编号

本文向大家介绍Dijkstra的Java算法，包括了Dijkstra的Java算法的使用技巧和注意事项，需要的朋友参考一下 Dijkstra的算法是一种用于在加权图中的节点之间找到最短路径的算法。创建图形时，我们将使用新的addEdge和addDirectedEdge方法向边缘添加权重。让我们看看这个算法是如何工作的- 创建一个距离集合，并将除源节点以外的所有顶点距离设置为无穷大。 当距离为0时，