《通信算法》专题
-
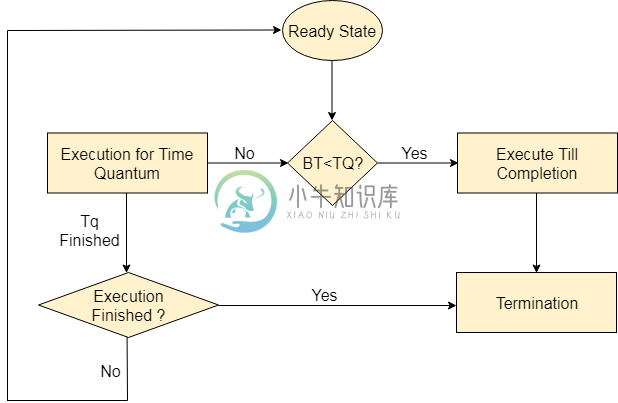 循环调度算法
循环调度算法主要内容:优点,缺点轮循调度算法是最流行的调度算法之一,它可以在大多数操作系统中实际实现。 这是先到先得的排程先发制人的版本。 该算法着重于时间共享。 在这个算法中,每个进程都以循环方式执行。 在称为时间量的系统中定义了一定的时间片。 就绪队列中的每个进程都分配给该时间段的CPU,如果在该时间内进程的执行完成,那么进程将终止,否则进程将返回就绪队列并等待下一轮完成 执行。 优点 它可以在系统中实际实现,因为它不依赖于
-
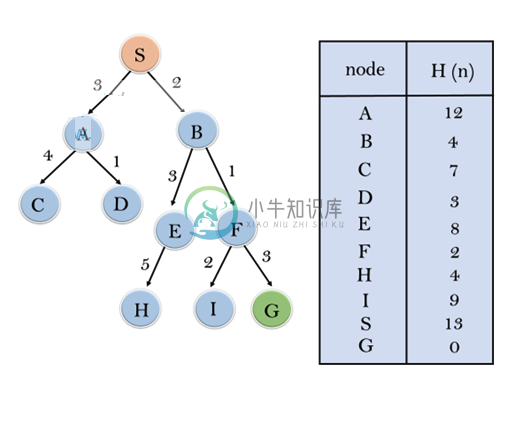 知情搜索算法
知情搜索算法主要内容:纯启发式搜索在前面章节中,我们已经讨论了不知情搜索算法,该搜索算法通过搜索空间查找问题的所有可能解决方案,而无需任何关于搜索空间的额外知识。但是,知情搜索(Informed Search)算法包含一系列知识,例如我们离目标有多远,路径成本,如何到达目标节点等。这些知识有助于代理人更少地探索搜索空间并更有效地找到目标节点。 知情搜索算法对于大型搜索空间更有用。知情搜索算法使用启发式思想,因此也称为启发式搜索。
-
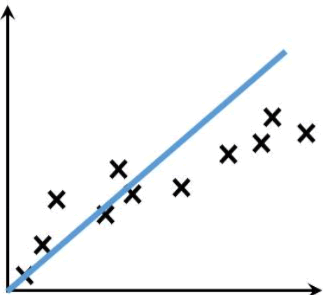 线性回归算法
线性回归算法主要内容:线性回归是什么,线性回归方程,实现预测的流程本节我们会认识第一个机器学习算法 —— 线性回归算法(Linear Regression),它是机器学习算法中较为简单,且容易理解的算法模型,你可以把它看做您的第一个“Hello World”程序。 我们先从语义上了解“线性回归”,如果您是第一次接触“线性回归”这个词,那么可以把它分开来看,其中“性代”表线性模型,而“回归”则表示回归问题,也就是用线性模型来解决回归问题。看完上述解释,您脑子中可能
-
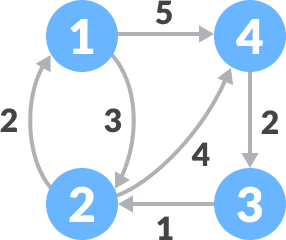 弗洛伊德算法
弗洛伊德算法主要内容:弗洛伊德算法的实现思路,弗洛伊德算法的具体实现在一个加权图中,如果想找到各个顶点之间的最短路径,可以考虑使用弗洛伊德算法。 弗洛伊德算法既适用于无向加权图,也适用于有向加权图。使用弗洛伊德算法查找最短路径时,只允许环路的权值为负数,其它路径的权值必须为非负数,否则算法执行过程会出错。 弗洛伊德算法的实现思路 弗洛伊德算法是基于 动态规划算法实现的,接下来我们以在图 1 所示的有向加权图中查找各个顶点之间的最短路径为例,讲解弗洛伊德算法的实现思
-
 最短路径算法
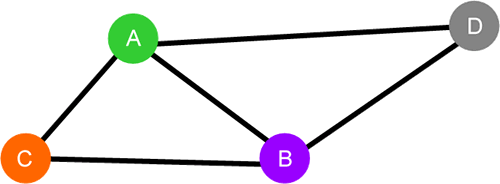
最短路径算法主要内容:最短路径算法在给定的图存储结构中,从某一顶点到另一个顶点所经过的多条边称为 路径。 图 1 图存储结构 例如在图 1 所示的图结构中,从顶点 A 到 B 的路径有多条,包括 A-B、A-C-B 和 A-D-B。当我们给图中的每条边赋予相应的权值后,就可以从众多路径中找出总权值最小的一条,这条路径就称为 最短路径。 图 2 无向带权图 以图 2 为例,从顶点 A 到 B 的路径有 3 条,它们各自的总权值是:
-
 哈希查找算法
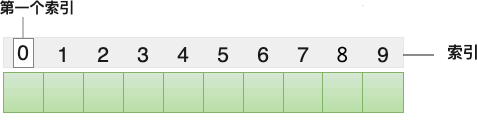
哈希查找算法主要内容:哈希表是什么,哈希查找算法哈希查找算法又称 散列查找算法,是一种借助哈希表(散列表)查找目标元素的方法,查找效率最高时对应的时间复杂度为 O(1)。 哈希查找算法适用于大多数场景,既支持在有序序列中查找目标元素,也支持在无序序列中查找目标元素。讲解哈希查找算法之前,我们首先要搞清楚什么是哈希表。 哈希表是什么 哈希表(Hash table)又称 散列表,是一种存储结构,通常用来存储多个元素。 和其它存储结构(线性表、树等)
-
 插值查找算法
插值查找算法主要内容:插值查找算法的解题思路,插值查找算法的具体实现插值查找算法又称 插值搜索算法,是在 二分查找算法的基础上改进得到的一种查找算法。 插值查找算法只适用于有序序列,换句话说,它只能在升序序列或者降序序列中查找目标元素。作为“改进版”的二分查找算法,当有序序列中的元素呈现均匀分布时,插值查找算法的查找效率要优于二分查找算法;反之,如果有序序列不满足均匀分布的特征,插值查找算法的查找效率不如二分查找算法。 所谓均匀分布,是指序列中各个相邻元素的差值近
-
 二分查找算法
二分查找算法主要内容:二分查找算法的实现思路,二分查找算法的具体实现二分查找又称 折半查找、 二分搜索、 折半搜索等,是在 分治算法基础上设计出来的查找算法,对应的时间复杂度为 。 二分查找算法仅适用于有序序列,它只能用在升序序列或者降序序列中查找目标元素。 二分查找算法的实现思路 在有序序列中,使用二分查找算法搜索目标元素的核心思想是:不断地缩小搜索区域,降低查找目标元素的难度。 以在升序序列中查找目标元素为例,二分查找算法的实现思路是: 初始状态下,将整个序列
-
 顺序查找算法
顺序查找算法主要内容:顺序查找算法的实现思路,顺序查找算法的具体实现顺序查找算法又称 顺序搜索算法或者 线性搜索算法,是所有查找算法中最基本、最简单的,对应的时间复杂度为 。 顺序查找算法适用于绝大多数场景,既可以在有序序列中查找目标元素,也可以在无序序列中查找目标元素。 顺序查找算法的实现思路 所谓顺序查找,指的是从待查找序列中的第一个元素开始,查看各个元素是否为要找的目标元素。 举个简单的例子,采用顺序查找算法在 {10,14,19,26,27,31,33,3
-
稳定排序算法
相信您已经掌握了很多种排序算法,比如冒泡排序、插入排序、希尔排序、选择排序等。这些排序算法中,有些是 "稳定" 的,有些是 "不稳定" 的。 给定的待排序序列中,经常会包含相同的元素,例如: 3 1 2 4 2 此序列中包含两个元素 2,为了区分它们,我们分别称它们为 "红 2" 和 "绿 2"。 评价一个排序算法是否稳定,是指该算法完成排序的同时,是否会改变序列中相同元素的相对位置。例如,上面序
-
 基数排序算法
基数排序算法主要内容:基数排序算法的实现细节,基数排序算法的代码实现在学会 计数排序算法的基础上,本节我们再学习一种排序算法,称为 基数排序算法。 基数排序算法适用于对多个整数或者多个字符串进行升序或降序排序,例如: 121, 432, 564, 23, 1, 45, 788 "zhangsan"、"lisi"、"wangwu" 一个整数由多个数字组成,例如 123 由 1、2、3 这 3 个数字组成;一个字符串由多个字符组成,例如 "lisi" 由 "l"、"i
-
 计数排序算法
计数排序算法主要内容:计数排序算法的实现思路,计数排序算法的具体实现通过统计序列中各个元素出现的次数,完成对整个序列的升序或降序排序,这样的排序算法称为 计数排序算法。 接下来,我们为您系统地讲解计数排序算法。 计数排序算法的实现思路 假设待排序序列为 {4, 2, 2, 8, 3, 3, 1},使用计数排序算法完成升序排序的过程为: 1) 找到序列中的最大值(用 max 表示)。对于 {4, 2, 2, 8, 3, 3, 1} 序列来说,最大值是 8。 2) 创
-
 快速排序算法
快速排序算法主要内容:快速排序算法的实现提到排序算法,多数人最先想到的就是快速排序算法。快速排序算法是在分治算法基础上设计出来的一种排序算法,和其它排序算法相比,快速排序算法具有效率高、耗费资源少、容易实现等优点。 快速排序算法的实现思路是: 从待排序序列中任选一个元素(假设为 pivot)作为中间元素,将所有比 pivot 小的元素移动到它的左边,所有比 pivot 大的元素移动到它的右边; pivot 左右两边的子序列看作是两个待排
-
 归并排序算法
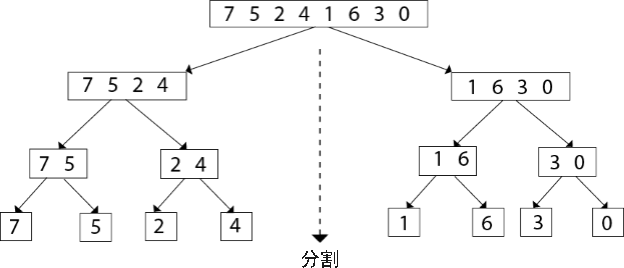
归并排序算法主要内容:归并排序算法的具体实现归并排序算法是在 分治算法基础上设计出来的一种排序算法,它可以对指定序列完成升序(由小到大)或降序(由大到小)排序,对应的时间复杂度为 。 归并排序算法实现排序的思路是: 将整个待排序序列划分成多个不可再分的子序列,每个子序列中仅有 1 个元素; 所有的子序列进行两两合并,合并过程中完成排序操作,最终合并得到的新序列就是有序序列。 举个简单的例子,使用归并排序算法对 {7, 5, 2, 4, 1,
-
 希尔排序算法
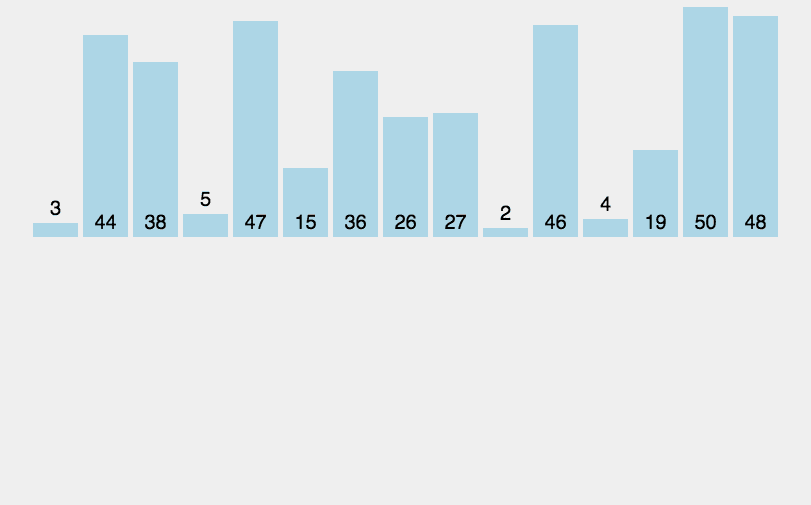
希尔排序算法主要内容:序列的划分方法,希尔排序算法的具体实现前面给大家介绍了 插入排序算法,通过将待排序序列中的元素逐个插入到有序的子序列中,最终使整个序列变得有序。下图所示的动画演示了插入排序的整个过程: 图 1 插入排序算法 观察动画不难发现,插入排序算法是通过比较元素大小和交换元素存储位置实现排序的,比较大小和移动元素的次数越多,算法的效率就越差。 希尔排序算法又叫 缩小增量排序算法,是一种更高效的插入排序算法。和普通的插入排序算法相比,希尔排序算法
