《贝壳》专题
-
 3.31贝壳前端一面 40min(凉)
3.31贝壳前端一面 40min(凉)小姐姐面的 全程态度很好(越感觉这样越凉) css盒模型 做一个两边宽高 自适应 面试官挺和蔼的 html语义化标签 js类型 基础类型和引用类型区分? 手撕闭包问题 vue加载有没有优化 答了大概有7种方式 webpack了解 最主要用了vite 箭头函数this指向 用户输入url加载页面到打开?这个基本背熟了hhh 浏览器渲染机制? http和https?加密流程 昨天看了一晚hhhhh w
-
Python基础教程之浅拷贝和深拷贝实例详解
本文向大家介绍Python基础教程之浅拷贝和深拷贝实例详解,包括了Python基础教程之浅拷贝和深拷贝实例详解的使用技巧和注意事项,需要的朋友参考一下 Python基础教程之浅拷贝和深拷贝实例详解 网上关于Python的深拷贝和浅拷贝的文章很多,这里对三种拷贝进行比较并附实例,大家可以参考下 一般的复制 通过以上实践会发现,复制操作就是将lista在内存中指向的地址,也让li
-
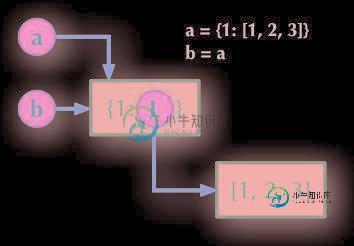 Python直接赋值、浅拷贝与深度拷贝实例分析
Python直接赋值、浅拷贝与深度拷贝实例分析本文向大家介绍Python直接赋值、浅拷贝与深度拷贝实例分析,包括了Python直接赋值、浅拷贝与深度拷贝实例分析的使用技巧和注意事项,需要的朋友参考一下 本文实例讲述了Python直接赋值、浅拷贝与深度拷贝。分享给大家供大家参考,具体如下: 直接赋值:其实就是对象的引用(别名)。 浅拷贝(copy):拷贝父对象,不会拷贝对象的内部的子对象。 深拷贝(deepcopy): copy 模块的 dee
-
Linux中拷贝 cp命令中拷贝所有的写法详解
本文向大家介绍Linux中拷贝 cp命令中拷贝所有的写法详解,包括了Linux中拷贝 cp命令中拷贝所有的写法详解的使用技巧和注意事项,需要的朋友参考一下 今天在编写一个脚本的时候,发现一个比较奇怪的问题:就是在使用cp拷贝当前目录下所有文件到目标目录的时候,源和目标目录大小不同。原来一直没有留意有这样的问题,后来查了些资料,才知道以前一直使用的格式有误, 一、预备 cp就是拷贝,最简单的使用方式
-
Java克隆浅拷贝深拷贝构造函数嵌套对象
我已经编写了一个测试应用程序,用于演示使用浅层、深层和复制构造函数的Java克隆。 我实现了浅和深,但与复制构造函数我认为我错过了一些东西。 请查看下面的代码,并让我知道复制构造函数实现的修复方法。 输出(复制构造函数) 15007 Amit Chirimiri Kripalu 15007 Amit Chirimiri ShriKrishn 编辑: 由于学生类包含嵌套类(教师)引用,简单的复制构造
-
朴素贝叶斯 - 为什么我们需要贝叶斯法则?
首先回顾一下贝叶斯公式: 再看看微软购物车的数据: 比如,我们为居住在邮编为88005地区的客户设置两个事件:买或不买Sencha绿茶,即: P(h1|D) = P(买绿茶|88005) P(h2|D) = P(┐买绿茶|88005) 你也许会问,这两个概率我们都可以直接从数据中计算得到,为什么还要计算下面这个公式呢? 那是因为在现实问题中要计算P(h|D)往往是很困难的。 以上一节中的医学示例来
-
再学贝叶斯网络 TAN 树型朴素贝叶斯算法
前言 在前面的时间里已经学习过了NB朴素贝叶斯算法, 又刚刚初步的学习了贝叶斯网络的一些基本概念和常用的计算方法。于是就有了上篇初识贝叶斯网络的文章,由于本人最近一直在研究学习<<贝叶斯网引论>>,也接触到了许多与贝叶斯网络相关的知识,可以说朴素贝叶斯算法这些只是我们所了解贝叶斯知识的很小的一部分。今天我要总结的学习成果就是基于NB算法的,叫做Tree Augmented Naive Bays,中
-
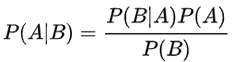 理解贝叶斯公式
理解贝叶斯公式主要内容:贝叶斯定理,条件概率,先验概率,后验概率,朴素+贝叶斯朴素贝叶斯(Naive Bayesian algorithm)是有监督学习的一种分类算法,它基于“贝叶斯定理”实现,该原理的提出人是英国著名数学家 托马斯·贝叶斯。贝叶斯定理是基于概率论和统计学的相关知识实现的,因此在正式学习“朴素贝叶斯算法”前,我们有必要先认识“贝叶斯定理”。 贝叶斯定理 贝叶斯定理的发明者 托马斯·贝叶斯 提出了一个很有意思的假设:“如果一个袋子中共有 10 个球,分别是黑
-
sendfile64仅拷贝2GB左右
我需要使用sendfile64来复制大约16GB的文件。到目前为止,我所取得的成就是 我使用 问题是我仍然无法复制超过2GB的文件。 有人能告诉我哪里错了吗?
-
赛贝斯查询迭代
我在临时表中填充了数据(该表最多将始终有 10 条记录)。我正在尝试的下一步是逐个拾取记录并查询数据库以测试某些条件并根据查询结果分配注释。例如: 我正在尝试编写一个sybase查询,它将一个接一个地拾取数据(递归地?),运行一些指定的查询并返回一个通过或失败的注释,然后我将最终填充到另一个临时表中 例如:第1行是AB1-从表中选择名称,其中name='AB1'如果它没有返回数据,我会停在那里并填
-
贝尔曼-福特算法
我知道Bellman-Ford算法最多需要| V |-1次迭代才能找到最短路径,如果图不包含负权重循环。有没有办法修改Bellman-Ford算法,使其在1次迭代中找到最短路径?
-
朴素贝叶斯代码
#encoding:utf-8 from numpy import * #词表到向量的转换函数 def loadDataSet(): postingList = [['my','dog','has','flea','problems','help','please'], ['maybe','not','take','him','to','dog',
-
三次贝塞尔曲线
bezierCurveTo()方法 绘制三次贝塞尔曲线代码如下。 context.bezierCurveTo(cp1x,cp1y,cp2x,cp2y,x,y); 这个方法可谓是绘制波浪线的神器。根据之前的结论,n阶贝塞尔曲线就有n-1个控制点,所以三次贝塞尔曲线有1个起始点、1个终止点、2个控制点。因此传入的6个参数分别为控制点cp1 (cp1x, cp1y),控制点cp2 (cp2x, cp2
-
二次贝塞尔曲线
贝塞尔曲线 Bézier curve(贝塞尔曲线)是应用于二维图形应用程序的数学曲线。 曲线定义:起始点、终止点、控制点。通过调整控制点,贝塞尔曲线的形状会发生变化。 1962年,法国数学家Pierre Bézier第一个研究了这种矢量绘制曲线的方法,并给出了详细的计算公式,因此按照这样的公式绘制出来的曲线就用他的姓氏来命名,称为贝塞尔曲线。 这里我们不介绍计算公式,只要知道贝塞尔曲线是一条由起始
-
初识贝叶斯网络
前言 一看到贝叶斯网络,马上让人联想到的是5个字,朴素贝叶斯,在所难免,NaiveByes的知名度确实会被贝叶斯网络算法更高一点。其实不管是朴素贝叶斯算法,还是今天我打算讲述的贝叶斯网络算法也罢,归根结底来说都是贝叶斯系列分类算法,他的核心思想就是基于概率学的知识进行分类判断,至于分类得到底准不准,大家尽可以自己用数据集去测试测试。OK,下面进入正题--贝叶斯网络算法。 朴素贝叶斯 一般我在介绍某
