javascript - 二叉树的删除为什么一定要返回更新后的子节点?
二叉树的删除为什么一定要返回更新后的子节点
... //二叉树的删除 remove(key) { this.removeNode(this.root, key) } removeNode(node, key) { if (node == null) { return null } if (this.compareFn(key, node.key) === Compare.less) { //本人疑惑的地方//tip2 this.removeNode(node.left, key) } else if (this.compareFn(key, node.key) === Compare.bigger) { this.removeNode(node.right, key) } else { //tip1 node = null } } } var mytree = new BST() mytree.insert(4) mytree.insert(5) mytree.insert(1) mytree.remove(1)我看到大家都是以下这么写二叉树的删除的,不明白的是我在tip2处将node.left传入removeNode函数之后,按照JavaScript复杂数据类型变量存的是栈中的地址,那么我在tip1处将key为1的这个节点赋值为null,也就是mytree.root.left这个节点赋值为Null之后,为什么它最终没有被赋值为null,而是要采用下面tip3的方式才能实现删除呢
removeNode(node,key){ if(node==null){ return null } if(this.compareFn(key,node.key)===Compare.less){ //都采用了赋值的方式,把更新后的子节点赋值给父节点要修改的地方 //tip3 node.left = this.removeNode(node.left,key) return node }else if(this.compareFn(key,node.key)===Compare.bigger){...1.以下是比较官方的写法
const Compare = { less:-1, bigger:1, equ:0 } class Node{ constructor(key){ this.key = key this.left = null this.right = null } } class BST { constructor(){ this.root = null } insert(key){ if(this.root==null){ this.root = new Node(key) }else{ this.insertNode(this.root,key) } } compareFn(a,b){ if(a===b){ return Compare.equ } return a<b?Compare.less:Compare.bigger } insertNode(node,key){ if(this.compareFn(key,node.key)===Compare.less){ if(node.left==null){ node.left = new Node(key) }else{ this.insertNode(node.left,key) } }else{ if(node.right==null){ node.right = new Node(key) }else{ this.insertNode(node.right,key) } } } //中序遍历 inOrderMap(callback){ this.inOrderMapNode(this.root,callback) } inOrderMapNode(node,callback){ if(node!=null){ this.inOrderMapNode(node.left,callback) callback(node.key) this.inOrderMapNode(node.right,callback) } } //先序遍历 preOrderMap(callback){ this.preOrderMapNode(this.root,callback) } preOrderMapNode(node,callback){ if(node!=null){ callback(node.key) this.preOrderMapNode(node.left,callback) this.preOrderMapNode(node.right,callback) } } //后序遍历 postOrderMap(callback){ this.postOrderMapNode(this.root,callback) } postOrderMapNode(node,callback){ if(node!=null){ this.postOrderMapNode(node.left,callback) this.postOrderMapNode(node.right,callback) callback(node.key) } } min(){ return this.minNode(this.root) } minNode(node){ let current = node while(current!=null && current.left!=null){ current = current.left } return current } max(){ return this.maxNode(this.root) } maxNode(node){ let current = node while(current!=null && current.right!=null){ current = current.right } return current } search(key){ return this.searchNode(this.root,key) } searchNode(node,key){ if(node===null){ return false } if(this.compareFn(key,node.key) === Compare.less){ return this.searchNode(node.left,key) }else if(this.compareFn(key,node.key) === Compare.bigger){ return this.searchNode(node.right,key) }else{ return true } } remove(key){ this.root = this.removeNode(this.root,key) } removeNode(node,key){ if(node==null){ return null } if(this.compareFn(key,node.key)===Compare.less){ node.left = this.removeNode(node.left,key) return node }else if(this.compareFn(key,node.key)===Compare.bigger){ node.right = this.removeNode(node.right,key) return node }else{ if(node.left==null && node.right==null){ node= null return node } if(node.left==null){ node = node.right return node }else if(node.right==null){ node = node.left return node } //找到最小, const target = this.minNode(node.right) node.key = target.key node.right = this.removeNode(node.right,target.key) return node } } } var mytree = new BST() mytree.insert(3) mytree.insert(2) mytree.insert(5) mytree.insert(4) mytree.insert(6)2.以下是我不明白的,为什么出错的写法的半成品
const Compare = { less: -1, bigger: 1, equal: 0 } class Node { //这个key就是树节点的值,同时也是这个节点的中值 constructor(key) { this.key = key this.left = null this.right = null } } class BST { constructor() { this.root = null } insert(key) { if (this.root == null) { this.root = new Node(key) } else { //这种写法是很普遍的,每次操作都单拎出来一个处理函数,这个处理函数必然是要传入根节点从头开始一个个下去找来操作的,insert就是对外开放的接口,而insertNode就是内部操作的函数,实际上也是因为这一部分是我们需要递归处理的函数,所以你必须单开一个操作,又比如二叉树的遍历,删除,查找如果你要选择递归的方法,都是要重新封装一个处理函数去不断的递归他的 this.insertNode(this.root, key) } } compareFn(a, b) { if (a === b) { return Compare.equal } return a < b ? Compare.less : Compare.bigger } insertNode(node, key) { if (this.compareFn(key, node.key) === Compare.less) { if (node.left == null) { node.left = new Node(key) } else { this.insertNode(node.left, key) } } else { if (node.right == null) { node.right = new Node(key) } else { this.insertNode(node.right, key) } } } //中序遍历 inOrderMap(callback) { this.inOrderMapNode(this.root, callback) } inOrderMapNode(node, callback) { if (node != null) { this.inOrderMapNode(node.left, callback) callback(node.key) this.inOrderMapNode(node.right, callback) } } //先序遍历 preOrderMap(callback) { this.preOrderMapNode(this.root, callback) } preOrderMapNode(node, callback) { if (node != null) { callback(node.key) this.preOrderMapNode(node.left, callback) this.preOrderMapNode(node.right, callback) } } //后序遍历 postOrderMap(callback) { this.postOrderMapNode(this.root, callback) } postOrderMapNode(node, callback) { if (node != null) { this.postOrderMapNode(node.left) this.postOrderMapNode(node.right) callback(node.key) } } //最小的肯定在最最左边,其实这里可以不用封住 min() { return this.minNode(this.root) } minNode(node) { let current = node while (current != null && current.left != null) { current = current.left } return current } //最大的肯定在最最右边,其实这里可以不用封住 max() { return this.maxNode(this.root) } maxNode(node) { let current = node //写这个current!=null并不是多此一举,因为如果根节点为null的话,null.undefined这种不符合规矩.会报错的,无法访问一个null的属性 while (current != null && current.right != null) { current = current.right } return current } //这个查询查的是有没有这个值,而不是返回这个值的节点,如果要返回这个值的节点,可以用current来承载,最后返回current search(key) { return this.searchNode(this.root, key) } searchNode(node, key) { if (node === null) { return false } if (this.compareFn(key, node.key) === Compare.less) { return this.searchNode(node.left, key) } else if (this.compareFn(key, node.key) === this.compareFn.bigger) { return this.searchNode(node.right, key) } else { return true } } //二叉树的删除 remove(key) { this.removeNode(this.root, key) } removeNode(node, key) { if (node == null) { return null } if (this.compareFn(key, node.key) === Compare.less) { this.removeNode(node.left, key) } else if (this.compareFn(key, node.key) === Compare.bigger) { this.removeNode(node.right, key) } else { node = null } } } var mytree = new BST() mytree.insert(4) mytree.insert(5) mytree.insert(1) mytree.remove(1)3.以下是我在调试的过程中的观察,在插入4,5,1,删除1的最后一步这里,node和要删除的节点的确是指向的同一个节点,为什么赋值为null影响不了呢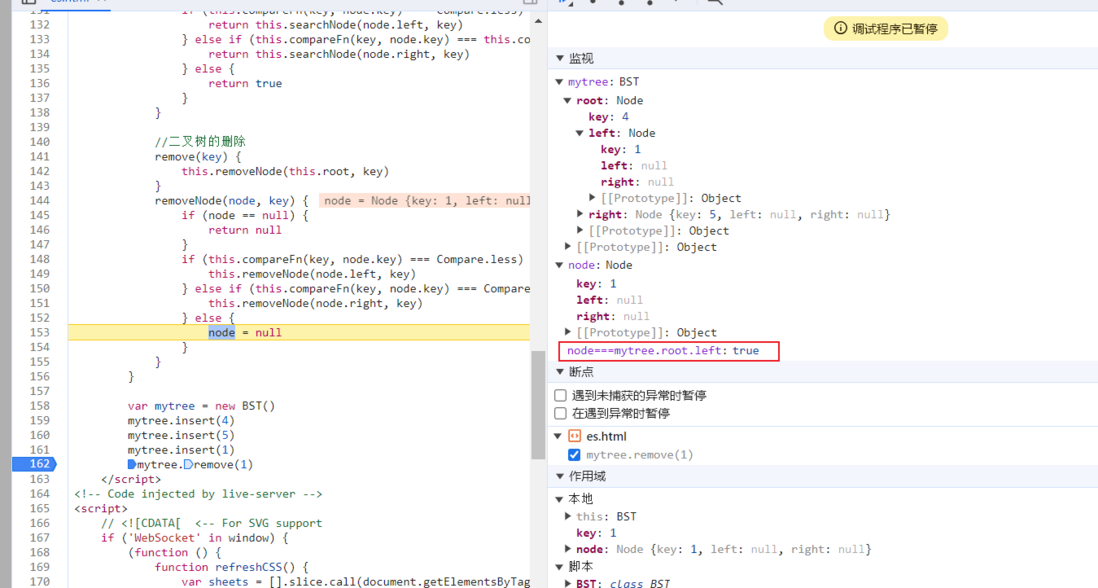
共有2个答案
没有仔细看代码,但是这里的node只是临时变量,把它置为null是没有用的。
比如
function setNull(value) { value = null;}var foo = new Object()foo.bar = "bar"setNull(foo);// foo 还是原来的值console.log(foo);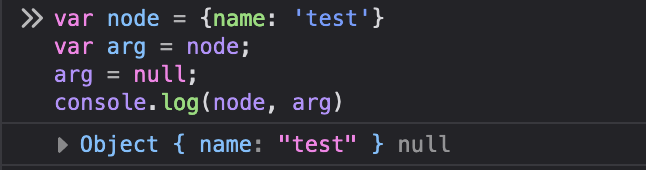
先看上面这段代码你能理解为什么node没有被赋值为null吗?当你把这个node传给一个函数的时候并且在函数内部对传入的参数做修改的话你想想是不是等同于上面这样;
的确引用类型存储的是指针,但是你对变量的赋值修改的是指针的指向,并不会修改另一个变量的指针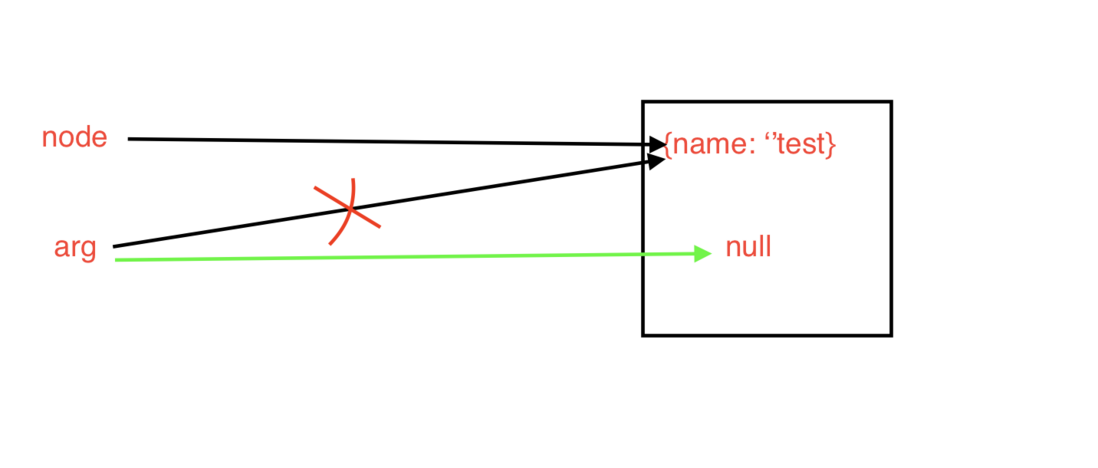
-
我现在正在读一本关于从二叉搜索树中删除节点的书,书中描述的过程对我来说似乎不必要地复杂。 在1号情况下,如果我们删除40,它将替换为30;在 2 号情况下,如果我们删除 40,它将被替换 35。 但在书中,它说应该从要删除的节点的右子树中找到替换,这可能涉及一些复杂的操作。 我在这里遗漏了什么吗?请指出。
-
我正在阅读一本书,该书解释了如何从二元搜索树中删除节点,基本上如果我们有这棵树: 我们想删除节点4,书上说我应该: 在其右子树(即6)中找到4的继任者 交换4和6 从右子树中删除6 将4的左侧子树(在本例中仅为1)附加到新节点6 因此我们得到 然而,我想到了另一种方法来做到这一点: 找到4个右子树的最小元素(即6) 将4的左子树附加到6(它不会有左子树) 将父元素(10)附加到4的右侧元素(8)。
-
当删除具有两个子节点的节点时,如果指示使用标准的二叉搜索树节点删除算法,我们应该将其替换为右子树的最小节点还是左子树的最大节点?
-
我的删除方法由4个if语句组成,用于处理二叉查找树中的4种不同类型的删除。不确定哪里错了,但当我检查它时,它没有删除任何节点。如果赞赏,任何帮助。提前感谢' 我怀疑问题在于我试图将节点删除替换为空 }
-
我有一个任务,我需要一些方法的帮助。 所以我有一棵这样的树: 而我的方法是: 讲师给出了树的一个简单实现。这个类叫做BinaryTree,如果您想让一个节点链接到它,那么您可以指定右子BinaryTree节点和左子BinaryTree节点。 一个节点有两个链接(一个指向左边,另一个指向右边的子节点),没有指向头部的链接。 因此,使用当前的方法,我能够成功地进行预购遍历,我通过编写存储在节点中的元素
-
在二元搜索树的情况下,为什么我们不能简单地在一个节点有两个子节点的情况下,将一个节点的前一个节点替换为后一个节点?

