当使用双打时，为什么(x/(y*z))与（x/y/z）不一样？[副本]

Question

这部分是学术性的，就我的目的而言，我只需要四舍五入到小数点后两位；但我很想知道发生了什么会产生两种略有不同的结果。

这是我编写的测试，将其缩小到最简单的实现：

@Test
public void shouldEqual() {
  double expected = 450.00d / (7d * 60);  // 1.0714285714285714
  double actual = 450.00d / 7d / 60;      // 1.0714285714285716

  assertThat(actual).isEqualTo(expected);
}

但它失败了，输出如下：

org.junit.ComparisonFailure: 
Expected :1.0714285714285714
Actual   :1.0714285714285716

有谁能详细解释一下是什么原因导致

我在一个答案中寻找的一些要点是：精度损失在哪里？哪种方法是首选的，为什么？哪一个实际上是正确的？（在纯数学中，不可能两者都是对的。也许两者都是错的？）对于这些算术运算，有没有更好的解决方案或方法？

Answer 1

我看到一堆问题告诉你如何解决这个问题，但没有一个真正解释了发生了什么，除了“浮点舍入错误很糟糕，好吗？”所以让我试试看。让我首先指出，这个答案中没有任何内容是特定于Java的。舍入误差是任何固定精度的数字表示所固有的问题，所以在C语言中也会遇到同样的问题。

作为一个简化的示例，假设我们有某种计算机在本地使用无符号十进制数据类型，我们将其称为float6d。数据类型的长度为6位：4位表示尾数，2位表示指数。例如，数字3.142可以表示为

3.142 x 10^0

以6位数字存储为

503142

前两位是指数加50，后四位是尾数。此数据类型可以表示从0.001×10^-50到9.999×10^+49的任意数字。

其实不是这样的。它不能存储任何数字。如果要表示3.141592呢？还是3.1412034？还是3.141488906？不幸的是，数据类型不能存储超过四位数的精度，所以编译器必须用更多的位数来四舍五入，以适应数据类型的约束。如果你写

float6d x = 3.141592;
float6d y = 3.1412034;
float6d z = 3.141488906;

然后，编译器将这三个值中的每一个转换为相同的内部表示形式:3.142x10^0（请记住，它存储为503142)，这样x==y==z将保持为真。

关键在于，有一个完整的实数范围，所有实数都映射到相同的潜在数字序列（或位，在一个真实的计算机中）。具体地说，满足3.1415<=x<=3.1425的任何x（假定为半舍入）都将转换为表示形式503142存储在内存中。

每次程序在内存中存储浮点值时都会发生这种舍入。第一次发生这种情况是在源代码中编写常量时，就像我在上面对X、Y和Z所做的那样。当您执行一个算术运算，将精度的位数增加到超出数据类型所能表示的范围时，这种情况再次发生。这两种影响中的任何一种都称为舍入误差。有几种不同的方式可以发生这种情况：

>

加减法：如果你要加的一个值的指数与另一个不同，你将得到额外的精度数字，如果有足够多的数字，最低有效的数字将需要删除。例如，2.718和121.0都是可以在float6d数据类型中精确表示的值。但是如果你试着把它们加在一起：

   1.210     x 10^2
+  0.02718   x 10^2
-------------------
   1.23718   x 10^2

取整为1.237x10^2或123.7，精度下降两位数。

乘法：结果中的位数近似为两个操作数中位数之和。如果操作数已经有许多有效数字，这将产生一定数量的舍入误差。例如，121 x 2.718为您提供了

   1.210     x 10^2
x  0.02718   x 10^2
-------------------
   3.28878   x 10^2

将其舍入为3.289x10^2或328.9，再次删除两位数的精度。

但是，请记住，如果操作数是“好”的数字，没有许多有效数字，浮点格式可能可以准确地表示结果，因此不必处理舍入误差。例如，2.3x140给出

   1.40      x 10^2
x  0.23      x 10^2
-------------------
   3.22      x 10^2

它没有舍入问题。

部门：这就是事情变得混乱的地方。除法通常会导致一定程度的舍入误差，除非你要除以的数字碰巧是基数的幂（在这种情况下，除法只是一个数字移位，或者二进制的位移位）。举个例子，取两个非常简单的数字，3和7，把它们除以，你就得到了

   3.                x 10^0
/  7.                x 10^0
----------------------------
   0.428571428571... x 10^0

可以表示为float6d的最接近该数字的值是4.286x10^-1或0.4286，这与精确结果明显不同。

正如我们将在下一节中看到的，舍入引入的错误随着您所做的每一个操作而增加。因此，如果您使用的是“好”的数字，如您的示例中所示，通常最好尽可能晚地进行除法操作，因为这些操作最有可能在您的程序中引入舍入错误，而以前没有舍入错误。

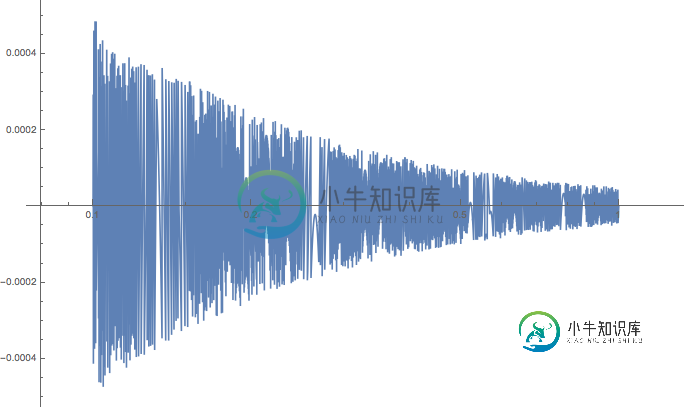
一般来说，如果你不能假设你的数字是“好的”，舍入误差可以是正的，也可以是负的，而且很难根据运算来预测它会向哪个方向发展。这取决于所涉及的具体价值。将2.718z的roundoff错误作为z的函数（仍然使用float6d数据类型）查看如下图：

实际上，当您处理使用数据类型的全部精度的值时，通常更容易将舍入错误视为随机错误。查看图中的内容，您可能能够猜测错误的大小取决于操作结果的数量级。在这种特殊情况下，当z的顺序为10^-1时，2.718z也是10^-1的顺序，因此它将是0.xxxx形式的数字。最大舍入误差是最后一位精度的一半；在这种情况下，“精度的最后一位数”是指0.0001，所以舍入误差在-0.00005和+0.00005之间变化。当2.718z跳到下一个数量级，即1/2.718=0.3679时，可以看到舍入误差也跳到了一个数量级。

您可以使用众所周知的误差分析技术来分析某个大小的随机（或不可预测）误差如何影响您的结果。具体地说，对于乘法或除法，结果中的“平均”相对误差可以通过将求积中每个操作数的相对误差相加来近似--也就是说，将它们平方，相加，然后取平方根。对于我们的float6d数据类型，相对误差在0.0005（对于像0.101这样的值）和0.00005（对于像0.995这样的值）之间变化。

让我们将0.0001作为X和Y值相对误差的粗略平均值。x*y或x/y中的相对误差由

sqrt(0.0001^2 + 0.0001^2) = 0.0001414

它是sqrt(2)的一个因子，大于每个单独值中的相对误差。

当涉及到组合操作时，您可以多次应用此公式，每个浮点操作一次。例如，对于z/(x*y)，x*y中的相对误差平均为0.0001414（在这个十进制示例中），然后z/(x*y)中的相对误差为

sqrt(0.0001^2 + 0.0001414^2) = 0.0001732

注意，平均相对误差随每次运算而增长，特别是乘法和除法次数的平方根。

类似地，对于z/x*y，z/x中的平均相对误差为0.0001414，z/x*y中的相对误差为

sqrt(0.0001414^2 + 0.0001^2) = 0.0001732

所以，同样的，在这种情况下。这意味着对于任意值，平均而言，这两个表达式引入的误差大致相同。（理论上是这样。我看到这些操作在实践中表现得非常不同，但那是另一回事。）

1.1100000000000000000000000000000000000000000000000000 x 2^00000000010
                       52 bits                             11 bits

前导的1没有显式存储，它构成第53位。另外，您应该注意存储的表示指数的11位实际上是实际指数加1023。例如，此特定值为7，即1.75x2²。二进制中的尾数为1.75，或者1.11，而二进制中的指数为1023+2=1025，或者10000000001，因此存储在内存中的内容为

01000000000111100000000000000000000000000000000000000000000000000
 ^          ^
 exponent   mantissa

但这并不重要。

你的例子还包括450，

1.1100001000000000000000000000000000000000000000000000 x 2^00000001000

和60，

1.1110000000000000000000000000000000000000000000000000 x 2^00000000101

您可以使用此转换器或Internet上的任何其他转换器来玩这些值。

在计算第一个表达式450/(7*60)时，处理器首先进行乘法运算，得到420或

1.1010010000000000000000000000000000000000000000000000 x 2^00000001000

1.0001001001001001001001001001001001001001001001001001001001001001001001...

二进制的。现在，Java语言规范说

不精确的结果必须四舍五入到最接近无限精确结果的可表示值；如果两个最近的可表示值相等接近，则选择其最低有效位为零的值。这是IEEE754标准的默认舍入模式，称为舍入到最近。

在64位IEEE 754格式中，最接近15/14的可表示值是

1.0001001001001001001001001001001001001001001001001001 x 2^00000000000

这大约是1.0714285714285714十进制。（更准确地说，这是唯一指定此特定二进制表示形式的最不精确的十进制值。）

另一方面，如果先计算450/7，结果是64.2857142857...，或者是二进制的，

1000000.01001001001001001001001001001001001001001001001001001001001001001...

其最近的可表示值为

1.0000000100100100100100100100100100100100100100100101 x 2^00000000110

1.000100100100100100100100100100100100100100100100100110011001100110011...

1.0001001001001001001001001001001001001001001001001010 x 2^00000000000

这与最后两位中的其他操作顺序不同：它们是10而不是01。小数等效值是1.0714285714285716。

如果您查看精确的二进制值，那么导致这种差异的特定舍入应该是清楚的：

1.0001001001001001001001001001001001001001001001001001001001001001001001...
1.0001001001001001001001001001001001001001001001001001100110011001100110...
                                                     ^ last bit of mantissa

在这种情况下，前一个结果，在数值上是15/14，碰巧是精确值的最准确表示。这是一个例子，说明了离开“组织”到最后是如何让你受益的。但是，这条规则只适用于您所使用的值没有使用数据类型的全部精度的情况。一旦开始处理不精确（舍入）值，就不再通过先进行乘法来防止进一步的舍入错误。