为什么statsmodels的OLS中的四次线性回归与LibreOffice Calc不匹配?
我正在使用statsmodels的OLS线性回归和Patsy四次公式y~xi(x**2)I(x**3)I(x**4),但得到的回归与LibreOffice Calc的数据相比不太吻合。为什么这与LibreOffice Calc的结果不匹配?
STATSAMDELS代码:
import io
import numpy
import pandas
import matplotlib
import matplotlib.offsetbox
import statsmodels.tools
import statsmodels.formula.api
csv_data = """Year,CrudeRate
1999,197.0
2000,196.5
2001,194.3
2002,193.7
2003,192.0
2004,189.2
2005,189.3
2006,187.6
2007,186.9
2008,186.0
2009,185.0
2010,186.2
2011,185.1
2012,185.6
2013,185.0
2014,185.6
2015,185.4
2016,185.1
2017,183.9
"""
df = pandas.read_csv(io.StringIO(csv_data))
cause = "Malignant neoplasms"
x = df["Year"].values
y = df["CrudeRate"].values
olsdata = {"x": x, "y": y}
formula = "y ~ x + I(x**2) + I(x**3) + I(x**4)"
model = statsmodels.formula.api.ols(formula, olsdata).fit()
print(model.params)
df.plot("Year", "CrudeRate", kind="scatter", grid=True, title="Deaths from {}".format(cause))
func = numpy.poly1d(model.params.values[::-1])
matplotlib.pyplot.plot(df["Year"], func(df["Year"]))
matplotlib.pyplot.show()
生成以下系数:
Intercept 9.091650e-08
x 9.127904e-05
I(x ** 2) 6.109623e-02
I(x ** 3) -6.059164e-05
I(x ** 4) 1.503399e-08
和下面的图表:
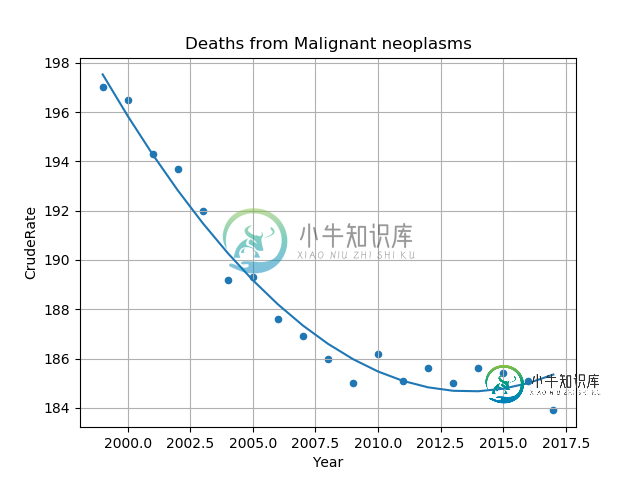
但是,如果我将数据放入LibreOffice Calc,请单击绘图并选择“插入趋势线…”,选择“多项式”,输入“度”=4,然后选择“显示方程”,得到的趋势线与statsmodels不同,似乎更接近:
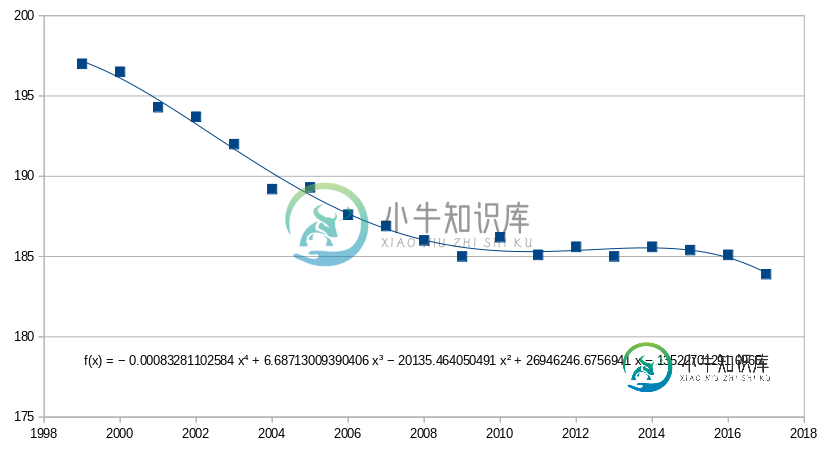
系数为:
Intercept = 1.35e10
x = 2.69e7
x^2 = -2.01e4
x^3 = 6.69
x^4 = -0.83e-3
statsmodels版本:
$ pip3 list | grep statsmodels
statsmodels 0.9.0
编辑:立方也不匹配,但二次匹配。
编辑:向下缩放年份(并在LibreOffice中执行相同操作)匹配:
df = pandas.read_csv(io.StringIO(csv_data))
df["Year"] = df["Year"] - 1998
缩小比例后的系数和绘图:
Intercept 197.762384
x -0.311548
I(x ** 2) -0.315944
I(x ** 3) 0.031304
I(x ** 4) -0.000833
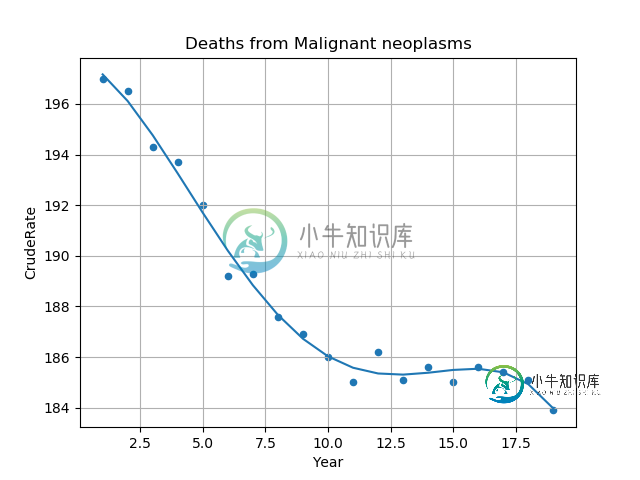
共有1个答案
根据@Josef的评论,问题在于大数不能处理高阶多项式,statsmodels不能自动缩放域。此外,我在最初的问题中没有提到这一点,因为我不希望域需要转换,但我还需要根据年份预测样本外值,因此我将其作为范围的结束:
predict_x = +5
min_scaled_domain = -1
max_scaled_domain = +1
df["Year"] = df["Year"].transform(lambda x: numpy.interp(x, (x.min(), x.max() + predict_x), (min_scaled_domain, max_scaled_domain)))
此转换创建了一个拟合良好的回归:
如果在LibreOffice Calc中应用了相同的域转换,则系数匹配。
最后,要打印预测值:
func = numpy.polynomial.Polynomial(model.params)
print(func(max_scaled_domain))
-
我试图拟合在库中实现的线性回归模型。 我对方法有疑问。假设我有大小为15的数据样本,我将其分为3部分,并拟合模型。调用每个将正确拟合模型或覆盖以前的值。
-
问题内容: 计量经济学背景 Fama Macbeth回归是指对面板数据进行回归的过程(其中有N个不同的个体,每个个体对应多个时期T,例如日,月,年)。因此,总共有N x T obs。请注意,如果面板数据不平衡,则可以。 Fama Macbeth回归法是对每个时期进行跨部门回归,即在给定时期t中将N个个体合并在一起。并针对t = 1,… T执行此操作。因此,总共进行了T回归。然后,对于每个自变量,我
-
本文向大家介绍LR与线性回归的区别?相关面试题,主要包含被问及LR与线性回归的区别?时的应答技巧和注意事项,需要的朋友参考一下 LR就是一种线性回归,经典线性回归模型的优化目标是最小二乘,而逻辑回归是似然函数,另外线性回归在整个实数域范围内进行预测,线性回归模型无法做到sigmoid的非线性形式,simoid可以轻松处理0/1分类问题
-
我正在运行我在buitin网站上看到的一个关于张量流线性回归的代码,它总是给我一个错误,我不知道代码有什么问题。首先我以为这是我的ide,然后当我切换到jupyter实验室时,它显示了我在这一点上的错误 首先我以为这是我的ide,然后当我切换到jupyter实验室时,它显示了我在这一点上的错误
-
线性回归是最简单的回归方法,它的目标是使用超平面拟合数据集,即学习一个线性模型以尽可能准确的预测实值输出标记。 单变量模型 模型 $$f(x)=w^Tx+b$$ 在线性回归问题中,一般使用最小二乘参数估计($$L_2$$损失),定义目标函数为 $$J={\arg min}{(w,b)}\sum{i=1}^{m}(y_i-wx_i-b)^2$$ 均方误差(MSE) $$MSE = \frac{1}{
-
线性回归输出是一个连续值,因此适用于回归问题。回归问题在实际中很常见,如预测房屋价格、气温、销售额等连续值的问题。与回归问题不同,分类问题中模型的最终输出是一个离散值。我们所说的图像分类、垃圾邮件识别、疾病检测等输出为离散值的问题都属于分类问题的范畴。softmax回归则适用于分类问题。 由于线性回归和softmax回归都是单层神经网络,它们涉及的概念和技术同样适用于大多数的深度学习模型。我们首先

