如何在O(n*log(n))时间内找到并打印n个给定圆的交点?
我正在寻找一个O(n*logn)算法来查找并打印n给定圆的交点。每个圆由其中心和半径指定。
O(n2)算法包括检查中心之间的距离是否小于或等于(被比较的两个圆的)半径之和。然而,我正在寻找一个更快的!
一个类似的问题是线段的相交。我想即使我的问题可以解决使用行扫描算法,但我无法弄清楚如何修改事件队列在情况下的圆。
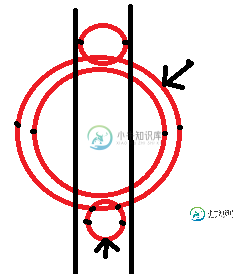
共有1个答案
行扫描算法只需在遇到左极值(即(x-r,y))时将圆添加到列表中,遇到右极值时将其从列表中删除。在向列表中添加圆圈之前,请对照列表中已有的圆圈进行检查。所以你的事件队列基本上是所有圆的左右极值,按X排序。(注意,您提前了解了所有的事件,所以这并不是真正意义上的正常意义上的“队列”。)
这也被称为“扫剪”。
-
描述一个O(n logn)-时间算法,给定一组由n个整数和另一个整数x组成的S,该算法确定S中是否存在两个元素,其和正好是x。 我计划用二进制搜索来搜索这个。 我如何找到这个算法的时间复杂度?如果T(n)不是(n log n),正确的算法是什么?
-
本文向大家介绍在C ++中找到(1 ^ n + 2 ^ n + 3 ^ n + 4 ^ n)mod 5,包括了在C ++中找到(1 ^ n + 2 ^ n + 3 ^ n + 4 ^ n)mod 5的使用技巧和注意事项,需要的朋友参考一下 在本教程中,我们将解决以下问题。 给定一个整数n,我们必须找到(1 n +2 n +3 n +4 n)%5 如果n大,则数字(1 n +2 n +3 n +4
-
我在GeekforGeekshttps://www.geeksforgeeks.org/minimum-number-of-jumps-to-reach-end-of-a-given-array/中检查“到达终点的最小跳跃次数”问题。我对这里提到的时间复杂度感到困惑,它是O(n^n)。 如果我看到上面的代码块,minJumps(arr,I,h)递归调用是从I=l1调用的。所以在每个递归步骤中,l(
-
我试图为这段代码找出一个大O的紧密界限: 如果我们从内最循环开始,它将在最坏的情况下运行k=n^2次,占O(N^2)。如果语句每次j=m*i时都为真,其中m是一个任意常数。由于j从1运行到i^2,这将在m={1,2,...,i}时发生,这意味着它将在i次时为真,i最多可以是n,所以最坏的情况将是m={1,2,...,n}=n次。如果i=n,第二个循环应该有O(N^2)的最坏情况。外环具有O(N)的
-
问题描述 (Problem Description) 如何打印数字总和? 解决方案 (Solution) 下面的示例演示了如何使用堆栈的概念添加前n个自然数。 import java.io.IOException; public class AdditionStack { static int num; static int ans; static Stack theStack;
-
家庭作业:寻找更好的策略或方法,而不是完整的代码。 当我试图确定这个问题的递归情况时,我完全被弄糊涂了。我必须编写一个接受整数参数“n”的方法,然后输出总共“n”个字符。根据原始整数是奇数还是偶数,中间字符应始终为“”或“*”。下面是两个不同的方法调用和输出应该是什么样子: 我该如何识别递归案例呢?

