树结构算法

Question

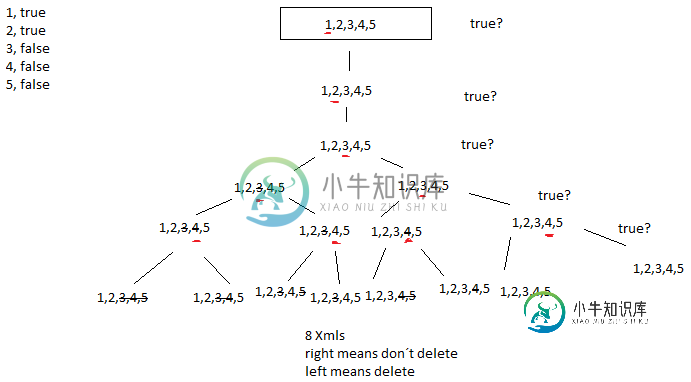
我的程序有问题。例如，我有5个字段。这些字段的值为true或false<代码>错误字段可以删除。所以我想找到这些领域的所有可能组合。

我的想法是：例如，我有一个包含这些字段的XML

• 字段1，正确
• 字段2，正确
• 字段3，错误
• 字段4，错误
• 第五场，错

结果应该是：

{Field1, Field2, Field3, Field4, Field5}
{Field1, Field2,       , Field4, Field5}
{Field1, Field2,       ,       , Field5}
{Field1, Field2,       ,       ,       }
{Field1, Field2, Field3,       , Field5}
{Field1, Field2, Field3,       ,       }
{Field1, Field2, Field3, Field4,       }
{Field1, Field2,       , Field4,       }

8种组合。

public List<List<Fieldmatrix>> permut(List<Fieldmatrix> matrix, int j) {

    while (felderLaenge != j) {

        if (!matrix.get(j).isTrue()) {
            tmpL = iterateLeft(matrix, j);

            tmpR = iterateRight(matrix, j);


        } else {
            tmpL = iterateRight(matrix, j);

        }
        j++;
        return permut(tmpL, j);
    }
    return sammlung;
}

iterateLeft表示删除，iterateRight表示不删除。

我无法实现复制功能。所以我只有4个Xmls结果：
{1,2,3,4,5}，{1,2,4,5}，{1,2,3,5}，{1,2,3,4}

有人能帮我吗？

首先，我感谢你的第一次支持。

字段矩阵类看起来像：

public class Fieldmatrix {

private String feld;
private boolean pflicht;

public Fieldmatrix(String feld, boolean pflicht){
    this.feld = feld;
    this.pflicht = pflicht;
}

public String getFeld() {
    return feld;
}

public void setFeld(String feld) {
    this.feld = feld;
}

public boolean isPflicht() {
    return pflicht;
}

public void setPflicht(boolean pflicht) {
    this.pflicht = pflicht;
}

}

我怎样才能改变这部分"prefix with Field.add（？）"你用String来处理它，这是可行的，因为List也是String的类型。但是我使用List。

iterateRight（）仅在控制台上打印。ieterateLeft（）删除当前字段并使用控制台打印。

Answer 1

存在多个问题：

• 如果当前树节点有两个子节点，则必须同时进入这两个节点，而不仅仅是左侧节点
• 最后，您返回了sammlung（engl.collection），但从未添加任何元素（至少不在呈现的代码中）
• 结合递归的while循环似乎有些奇怪。但是我不能在不看iterateLeft和iterateRight的情况下谈论这一点

实现该函数的快速方法如下。为了简单起见，Fieldmate类被String替换。

public static List<List<String>> combine(List<String> fields) {
    return combine(fields, 0, new ArrayList<>());
}

public static List<List<String>> combine(List<String> fields,
                                         int start, List<String> prefix) {
    List<List<String>> combinations = new ArrayList<>();
    if (start >= fields.size()) {
        combinations.add(prefix);
        return combinations;
    }
    String field = fields.get(start);
    if (field.contains("false")) {
        combinations.addAll(combine(fields, start + 1, prefix));
    }
    List<String> prefixWithField = new ArrayList<>(prefix);
    prefixWithField.add(field);
    combinations.addAll(combine(fields, start + 1, prefixWithField));
    return combinations;
}

这种实现效率不高。许多中间结果被一次又一次地复制。

List<String> fields = new ArrayList<>();
fields.add("1:true");
fields.add("2:true");
fields.add("3:false");
fields.add("4:false");
fields.add("5:false");
combine(fields).forEach(c -> System.out.println(c));

印刷品

[1:true, 2:true]
[1:true, 2:true, 5:false]
[1:true, 2:true, 4:false]
[1:true, 2:true, 4:false, 5:false]
[1:true, 2:true, 3:false]
[1:true, 2:true, 3:false, 5:false]
[1:true, 2:true, 3:false, 4:false]
[1:true, 2:true, 3:false, 4:false, 5:false]