算法代码优化：查找Equilibirum：在数组中查找一个索引，使其前缀和等于后缀和

Question

以下是我的任务描述：

给出了一个由N个整数组成的零索引数组。

这个数组的平衡指数是任意整数P，0≤ P

假设零元素之和等于0。如果P=0或P=N，则可能发生这种情况−1、例如，考虑下面的数组A，由n＝8个元素组成：

A[0] = -1
A[1] =  3
A[2] = -4
A[3] =  5
A[4] =  1
A[5] = -6
A[6] =  2
A[7] =  1

P = 1 is an equilibrium index of this array, because:
•   A[0] = −1 = A[2] + A[3] + A[4] + A[5] + A[6] + A[7]
P = 3 is an equilibrium index of this array, because:
•   A[0] + A[1] + A[2] = −2 = A[4] + A[5] + A[6] + A[7]
P = 7 is also an equilibrium index, because:
•   A[0] + A[1] + A[2] + A[3] + A[4] + A[5] + A[6] = 0

没有指数大于7的元素。P=8不是平衡指数，因为它不满足0≤P的条件

编写一个函数：int solution（NSMutableArray*a）；给定一个由N个整数组成的零索引数组a，它返回其任何平衡索引。

如果不存在平衡索引，函数应该返回−1。例如，给定上面显示的数组A，函数可以返回1、3或7，如上所述。

假设：•N是[0..100000]范围内的整数数组A的每个元素都是范围内的整数[−2,147,483,648..2,147,483,647].

复杂度：•预计最坏情况下的时间复杂度为O（N）；•预计最坏情况下的空间复杂度为O（N），超出了输入存储空间（不计算输入参数所需的存储空间）。

可以修改输入数组的元素。

以下是我对目标C中问题的解决方案：

-(int)solution:(NSArray *) A{
for (int i=0; i<A.count; i++) {

    NSUInteger backwardsTotal = 0;
    if (i > 0) {
        for (int k=0; k<i; k++) {
            NSNumber *kValue = A[k];
            backwardsTotal += kValue.intValue;
        }
    }

    NSUInteger forwardTotal = 0;
    for (int j=i+1; j<A.count; j++) {
        NSNumber *jValue = A[j];
        forwardTotal += jValue.intValue;
    }

    if (backwardsTotal == forwardTotal) {
        return i;
    }
}

return -1;
}

如何优化此解决方案？

根据@Nikki评论对方法所做的更改：

-(int)solution:(NSArray *) A{
NSUInteger a = 0, b = 0;

for (int i=0; i<A.count; i++) {
    NSNumber *iValue = A[i];
    b += iValue.intValue;
}
NSLog(@"Total: b: %ld", b);

for (int k=0; k<A.count; k++) {
    NSNumber *kValue = A[k];
    b -= kValue.intValue;

    NSLog(@"b: %ld", b);
    NSLog(@"a: %ld", a);

    if (a == b)
        return k;

    a += kValue.intValue;

}

return -1;
}

我正在测试上述代码如下：

//    NSArray *array = @[@"-3", @"0", @"3"];
NSArray *array = @[@"-2", @"4", @"-5", @"6", @"1", @"-6", @"2", @"1"];
NSUInteger one = [self solution:array];
NSLog(@"one: %ld", one);//returns 7

这个解决方案似乎效果更好。但它仍然不是完美的，并且使用O（N**2）时间复杂度。在其他性能测试中也存在超时错误。

以下截图：

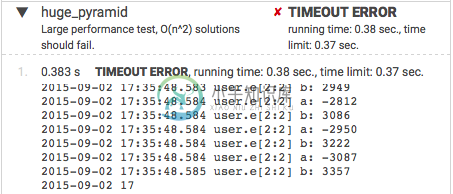
这还能优化吗？

Answer 1

官方C解决方案从Codness

http://blog.codility.com/2011/03/solutions-for-task-equi.html

int equi(int arr[], int n) {
    if (n==0) return -1; 
    long long sum = 0;
    int i; 
    for(i=0;i<n;i++) sum+=(long long) arr[i]; 

    long long sum_left = 0;    
    for(i=0;i<n;i++) {
        long long sum_right = sum - sum_left - (long long) arr[i];
        if (sum_left == sum_right) return i;
        sum_left += (long long) arr[i];
    } 
    return -1; 
} 

需要注意的两点：

• long long用于防止溢出。这已经足够了，因为在https://stackoverflow.com/a/37124098/895245中提到的最小尺寸保证以及代码的输入
• 注意n==0特殊情况

其他语言：

• Javahttps://stackoverflow.com/questions/21176777/codility-equilibrium-index-sample-test-my-stab-at-it
• C#更快实现sum（用于代码性测试）
• Python索引在数组中，使其前缀和等于后缀和-最佳解决方案

Answer 2

这个怎么样，希望对你有用...

int equi(int arr[], int n) {
if (n==0) return -1; 
long long sum = 0;
int i; 
for(i=0;i<n;i++) sum+=(long long) arr[i]; 

long long sum_left = 0;    
for(i=0;i<n;i++) {
    long long sum_right = sum - sum_left - (long long) arr[i];
    if (sum_left == sum_right) return i;
    sum_left += (long long) arr[i];
} 
return -1; 
} 

Answer 3

当前的解决方案是O（n^2）运算（将整个数组求和n次）。

在任意一点上都可以有两个变量，a和b，将a设置为零，b设置为数组的和。然后，迭代所有索引。在索引i上迭代时，首先执行b-=arr[i]。然后，如果a==b，返回i。然后执行a=arr[i]。这就是O（n）操作，效率更高。