如何找到每一棵树都跨越另一棵树的树集？

Question

假设给定一组树ST，每棵树的每个顶点都被标记。另外还给出了另一棵树T（也有顶点标签）。问题是如何找到ST的哪些树可以从T的根开始跨越树T，从而使生成树T的顶点标签与T的顶点标签一致。请注意，T的每个顶点的子节点要么完全覆盖，要么根本不覆盖——不允许部分覆盖子节点。换句话说：给定一棵树和以下过程：选择一个顶点，删除该顶点以下的所有顶点和边（除了顶点本身）。找到ST的那些树，这样每棵树都是用一系列应用于T的过程生成的。例如，给定树T

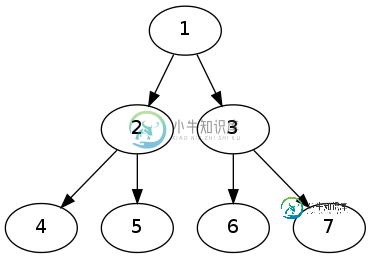
那些树

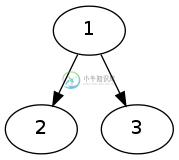
盖住T和树

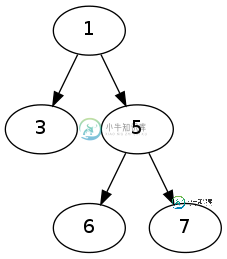
不是因为这棵树有3，5个孩子，而T有2，3个孩子。我能想到的最好的办法是要么用暴力强迫它，要么找到一组树，每个树都有与T相同的根标签，然后在这些树中搜索答案，但我想这两种方法都不是最佳方法。我想用某种方法把树砍掉，但什么也没出来。有什么想法吗？

笔记：

• 这些树不一定是二进制的
• 如果一棵树与另一棵树同根，那么它可以覆盖另一棵树
• 树是有序的，这意味着你不能交换任何两个孩子的位置

TL；DR-Find一个高效的算法，该算法在给定树T的查询中，从给定（固定/静态）集ST中找到能够覆盖T的所有树。

Answer 1

要验证一棵树是否覆盖了另一棵树，必须至少查看第一棵树的所有顶点一次。通过查看第一棵树的所有顶点来验证一棵树是否覆盖了另一棵树是微不足道的。因此，如果只需要检查一棵树，最简单的算法就已经是最优的了。

下面的一切都是我病态想象力的未经测试的果实。

如果有许多可能的T必须对照相同的ST进行检查，那么可以将ST的树存储为如下事实集

root = 1
children of node 1 = (2, 3)
children of node 2 = ()
children of node 3 = ()

这些事实可以存储在两个表中的标准关系数据库中，“根”（字段“树”和“根节点”）和“分支”（字段“树”、“节点”和“子节点”）。然后可以构建一个SQL查询或一系列查询来快速找到匹配的树。我的SQL fu是基本的，所以我无法在单个查询中管理它，但我相信这应该是可能的。

Answer 2

我将草图一个答案，然后提供一些工作的源代码。

首先，你需要一个算法来散列一棵树。我们可以假设，在不丧失一般性的情况下，树中每个节点的子节点都是从最小到最大排序的（反之亦然）。

在ST的每个成员上运行此算法并保存哈希值。

现在，以测试树T为例，生成保留原始根的所有子树TP。您可以通过以下方式实现此目的（可能效率低下）：

1. 使其节点的集合S
2. 生成S的功率集P
3. 通过从T的副本中删除P的每个成员中存在的节点来生成子树
4. 添加那些保留原始根的子树到TP。

现在生成一组TP的所有哈希。

现在检查每个ST哈希值是否为TP的成员。

ST哈希存储需要ST中的O（n）空间，可能还需要容纳树的空间。

您可以优化成员代码，使其不需要存储空间（我在测试代码中没有这样做）。代码将需要大约2N次检查，其中N是**T中的节点数。

因此，该算法在O（h2**N）中运行，其中H是ST的大小，N是T中的节点数。提高速度的最佳方法是找到一种改进的算法来生成T的子树。

以下Python代码实现了这一点：

#!/usr/bin/python
import itertools
import treelib
import Crypto.Hash.SHA
import copy

#Generate a hash of a tree by recursively hashing children
def HashTree(tree):
  digester=Crypto.Hash.SHA.new()

  digester.update(str(tree.get_node(tree.root).tag))

  children=tree.get_node(tree.root).fpointer
  children.sort(key=lambda x: tree.get_node(x).tag, cmp=lambda x,y:x-y)

  hash=False
  if children:
    for child in children:
      digester.update(HashTree(tree.subtree(child)))
    hash = "1"+digester.hexdigest()
  else:
    hash = "0"+digester.hexdigest()

  return hash

#Generate a power set of a set
def powerset(iterable):
  "powerset([1,2,3]) --> () (1,) (2,) (3,) (1,2) (1,3) (2,3) (1,2,3)"
  s = list(iterable)
  return itertools.chain.from_iterable(itertools.combinations(s, r) for r in range(len(s)+1))

#Generate all the subsets of a tree which still share the original root
#by using a power set of all the tree's nodes to remove nodes from the tree
def TreePowerSet(tree):
  nodes=[x.identifier for x in tree.nodes.values()]
  ret=[]
  for s in powerset(nodes):
    culled_tree=copy.deepcopy(tree)
    for n in s:
      try:
        culled_tree.remove_node(n)
      except:
        pass
    if len([x.identifier for x in culled_tree.nodes.values()])>0:
      ret.append(culled_tree)

  return ret

def main():
  ST=[]

  #Generate a member of ST
  treeA = treelib.Tree()
  treeA.create_node(1,1)
  treeA.create_node(2,2,parent=1)
  treeA.create_node(3,3,parent=1)
  ST.append(treeA)

  #Generate a member of ST
  treeB = treelib.Tree()
  treeB.create_node(1,1)
  treeB.create_node(2,2,parent=1)
  treeB.create_node(3,3,parent=1)
  treeB.create_node(4,4,parent=2)
  treeB.create_node(5,5,parent=2)
  ST.append(treeB)

  #Generate hashes for members of ST
  hashes=[(HashTree(tree), tree) for tree in ST]

  print hashes

  #Generate a test tree
  T=treelib.Tree()
  T.create_node(1,1)
  T.create_node(2,2,parent=1)
  T.create_node(3,3,parent=1)
  T.create_node(4,4,parent=2)
  T.create_node(5,5,parent=2)
  T.create_node(6,6,parent=3)
  T.create_node(7,7,parent=3)

  #Generate all the subtrees of this tree which still retain the original root
  Tsets=TreePowerSet(T)

  #Hash all of the subtrees
  Thashes=set([HashTree(x) for x in Tsets])

  #For each member of ST, check to see if that member is present in the test
  #tree
  for hash in hashes:
    if hash[0] in Thashes:
      print [x for x in hash[1].expand_tree()]

main()