在连通图中最大化可割边数
这个问题与LeetCode在网络中的关键连接非常相似。给定一个无向图,我们想要找到所有的桥。无向连通图中的一条边是一个桥,如果去掉它就会断开图的连接。
变体
而不是找到所有的桥,我想最大限度的边的数量,以删除,使图保持连接。
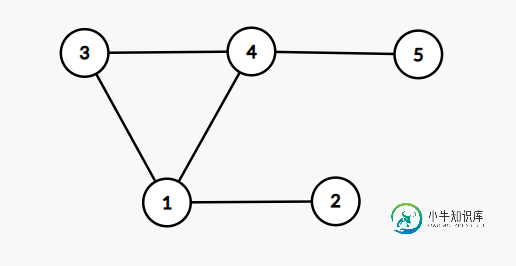
实施例2
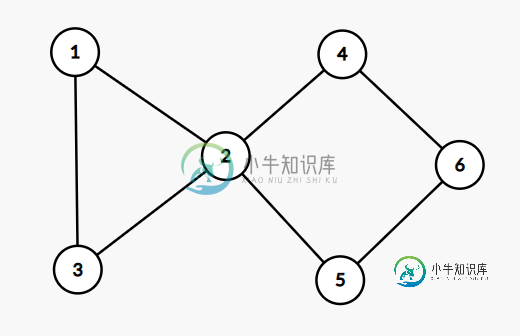
输出:2
共有1个答案
这很容易,如果我们在连通图中有e边和n节点,我们可以移除e-n+1边,使图保持连通。
如何做到这一点?:
只要做DFS/BFS就可以找到图的任何生成树,因为生成树是连通的,所以我们可以去掉所有其他的边。
-
对于算法的最终审查,出现了这样一个问题: 由于连通组件本质上是图中的一个图,这意味着子图中的所有顶点必须从较大的图中移除,同时保持内部连通性。我能理解这种直觉,但很难把它转化成一个公式。 到目前为止,我得出的结论如下: 对于连通分量n,每个图Gn具有相应的顶点集{Vn},使得顶点集的内容在内部连接,而在外部保持不连接。 现在,每个{Vn}最多包含V*(V-1)条边。 如何用公式表示最大边数?
-
考虑一个不连通的有向图的例子,其中顶点和边其中顶点是孤立的。 根据这里的答案:(对强连通图的最小加法),保证这个图所需的最小边数结果是3。 如何找到将这些边添加到哪里,即图中一条边的起始点和终止点?
-
无向图有n个顶点和0条边。我们能画出的最大边数是多少,这样图形就保持断开连接。 我已经给出了一个解决方案,我们可以排除一个顶点,并且可以找到无向图的n-1个顶点之间的最大边数,这样图仍然保持不连通。 对于n个顶点为n(n-1)/2,对于n-1个顶点为(n-1)(n-2)/2。有更好的解决办法吗?
-
背景:我是图论的新手,特别是“图割”。请不要太技术和速度。谢谢。 假设我有一个加权无向连通图G=(V,E)。我有一个变量a,它包含一个整数值,我想从图G中删除/裁剪所有权重低于a值的边。 问题1:如果图论中已经存在这一点(我看到了max-cut、min-cut、s-t cut,等等),它怎么称呼? 问题2:我如何使用数学符号正式表达/定义这种方法。 谢谢你的建议。
-
我想用最大流算法(Edmond Karp/Ford-Fulkerson算法)找到一个无向图的边连通性(即为了断开一个图而要去除的最小边数), 我知道我可以通过找到图的每两个节点之间的最小最大流来完成这个任务,但这将导致O(V^2)个流网络, 但我希望使用V个流网络(只运行O(V)次max flow算法)而不是O(V^2)个
-
以下是完整的问题: null 我的两个问题是:(1)在最小化SCCs之间的边之前的算法是正确的吗?(2)如何使SCC之间的边最小化。 对于(2),我知道这相当于使DAG中的边数最小化。(将SCCs视为顶点)。但这似乎对我没有帮助。

