Java中一种完全二叉搜索树的层次顺序插入

Question

我们有一个任务需要编码：

>

二叉搜索树

树必须是完整的，而不是完美的（这意味着不在最底层或次底层的所有节点都应该有两个子节点，而最底层的节点应该尽可能靠左）

我们需要按级别顺序插入树

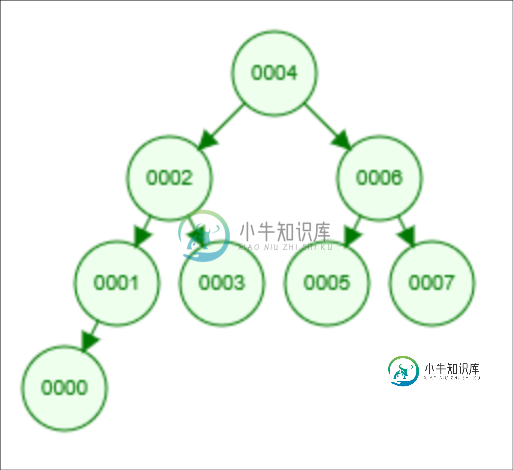
因此，如果我有一个包含元素{0,1,2,3,4,5,6,7}的数组，根应该是4，左边是2,1,3,0，右边是6,5,7。

插入的级别顺序为:4,2,6,1,3,5,7,0

只是取数组的中间并将其作为root是行不通的。如果您得到一个由1到9个元素组成的数组，那么您将有4个元素作为根（java中的int值，double将是4.5)，您将有5个元素在右侧，4个元素在左侧。这不是一棵完整的树。甚至不是一棵完美的树。

我的代码只能在左或右插入，这取决于它是否大于或小于根，没有级别顺序插入。anytypex参数是要插入的值，而binarynodet是我们在树中的当前节点（这是我们在需要向左或向右插入新值时进行比较的方式）

private BinaryNode<AnyType> insert( AnyType x, BinaryNode<AnyType> t )
{
    if( t == null )
        return new BinaryNode<>( x, null, null );

    int compareResult = x.compareTo( t.element );

    if( compareResult < 0 )
        t.left = insert( x, t.left );
    else if( compareResult > 0 )
        t.right = insert( x, t.right );
    else
        ;  // Duplicate; do nothing
    return t;
}

如何才能以级别顺序插入，并且仍然保持一个二叉搜索树？我应该使用某种形式的递归吗？

我的整个计划

import java.nio.BufferUnderflowException;
import java.util.*;

import static java.lang.Math.pow;

/**
 * Implements an unbalanced binary search tree.
 * Note that all "matching" is based on the compareTo method.
 * @author Mark Allen Weiss
 */
public class BinarySearchTree<AnyType extends Comparable<? super AnyType>>
{
    /**
     * Construct the tree.
     */
    public BinarySearchTree( )
    {
        root = null;
    }

    /**
     * Insert into the tree; duplicates are ignored.
     * @param x the item to insert.
     */
    public void insert( AnyType x )
    {
        root = insert( x, root );
    }

    /**
     * Test if the tree is logically empty.
     * @return true if empty, false otherwise.
     */
    public boolean isEmpty( )
    {
        return root == null;
    }

    /**
     * Print the tree contents in sorted order.
     */
    public void printTree( )
    {
        if( isEmpty( ) )
            System.out.println( "Empty tree" );
        else
            printTree( root );
    }

    /**
     * Internal method to insert into a subtree.
     * @param x the item to insert.
     * @param t the node that roots the subtree.
     * @return the new root of the subtree.
     */
    private BinaryNode<AnyType> insert( AnyType x, BinaryNode<AnyType> t )
    {
        if( t == null )
            return new BinaryNode<>( x, null, null );

        int compareResult = x.compareTo( t.element );

        if( compareResult < 0 )
            t.left = insert( x, t.left );
        else if( compareResult > 0 )
            t.right = insert( x, t.right );
        else
            ;  // Duplicate; do nothing
        return t;
    }

    /**
     * Internal method to print a subtree in sorted order.
     * @param t the node that roots the subtree.
     */
    private void printTree( BinaryNode<AnyType> t )
    {
        if( t != null )
        {
            printTree( t.left );
            System.out.println( t.element );
            printTree( t.right );
        }
    }

    /**
     * Internal method to compute height of a subtree.
     * @param t the node that roots the subtree.
     */
    private int height( BinaryNode<AnyType> t )
    {
        if( t == null )
            return -1;
        else
            return 1 + Math.max( height( t.left ), height( t.right ) );    
    }

    // Basic node stored in unbalanced binary search trees
    private static class BinaryNode<AnyType>
    {
            // Constructors
        BinaryNode( AnyType theElement )
        {
            this( theElement, null, null );
        }

        BinaryNode( AnyType theElement, BinaryNode<AnyType> lt, BinaryNode<AnyType> rt )
        {
            element  = theElement;
            left     = lt;
            right    = rt;
        }

        AnyType element;            // The data in the node
        BinaryNode<AnyType> left;   // Left child
        BinaryNode<AnyType> right;  // Right child
    }

      /** The tree root. */
    private BinaryNode<AnyType> root;

        // Test program
    public static void main( String [ ] args )
    {
        BinarySearchTree<Integer> t = new BinarySearchTree<>( );

        t.insert(2);
        t.insert(1);
        t.insert(3);
        t.printTree();
    }
}

Answer 1

完整的BST部分花了一点时间来理清它到底是什么。您的需求还需要订单级别的插入。我不能说这做了“插入”，但它建立了秩序级别的BST。

必须首先对输入列表进行排序。

构建顺序级别是通过以下方式完成的：取根并将其添加到BST中，然后将左列表拆分为左列表和右列表，将它们添加到列表列表中，然后处理列表列表。每一轮对列表的拆分和添加都是一个级别的插入。

好像管用。

public class Node<T extends Comparable<T>> {
    protected Node<T> left;
    protected Node<T> right;
    protected T data;   
}

public class BTree<T extends Comparable<T>> {
    private Node<T> root = new Node<>();
    public void addData(T data) {
        Node<T> parent = root;
        while (parent.data != null ) {
            if ( data.compareTo( parent.data ) > 0 ) {
                if ( parent.right == null ) 
                    parent.right = new Node<>();
                parent = parent.right;
            } else {
                if ( parent.left == null ) 
                    parent.left = new Node<>();
                parent = parent.left;
            }
        }
        parent.data = data;
    }
}

private void run() {
    for ( int i = 2; i < 65; ++i ) {
        List<Integer> intList = IntStream.range(1, i).boxed().collect(Collectors.toList());
        BTree<Integer> bTree = new BTree<>();
        List<List<Integer>> splitLists = new ArrayList<>();
        splitLists.add(intList);
        while (splitLists.size() > 0 ) {
            List<List<Integer>> tSplitLists = new ArrayList<>();
            for ( List<Integer> tIntList: splitLists) {
                int length = tIntList.size();
                // compute starting point
                int mid = calcMid(length);      // length/2 ; //+ calcOffset(length);
                bTree.addData(tIntList.get(mid));
                if ( mid - 0 > 0)
                    tSplitLists.add(tIntList.subList(0, mid));
                if ( length - (mid+1) > 0)
                    tSplitLists.add(tIntList.subList(mid+1, length));
            }
            splitLists = tSplitLists;
        }
        bTree.printNode();
    }
}
private int calcMid(int length) {
    if ( length <= 4 )
        return length / 2;
    int levelSize = 1;
    int total = 1;
    while ( total < length ) {
        levelSize *= 2;
        total += levelSize;
    }
    int excess = length - (total - levelSize);
    int minMid = (total - levelSize + 1) / 2;
    if ( excess <= levelSize / 2 ) {
        return minMid + (excess - 1); 
    } else {
        int midExcess = levelSize/2; 
        return minMid + (midExcess - 1);
    }

}

查看如何打印二叉树图？用于打印二叉树的代码。

ps>我相信你可以通过清除和复制列表而不是每次都创建新的列表来使它变得更好。

1 

 2   
/   
1   

 2   
/ \ 
1 3

   3       
  / \   
 /   \  
 2   4   
/       
1