在张力流概率中具有 3 个隐藏密集层的回归模型在训练期间返回 nan 作为损失

Question

我开始熟悉张量流概率，在这里我遇到了一个问题。在训练期间，模型返回nan作为损失(可能意味着导致溢出的巨大损失)。由于合成数据的函数形式并不过分复杂，并且数据点与参数的比率乍一看并不可怕，至少我想知道问题出在哪里，以及如何纠正它。

代码如下 --附有一些可能有用的图像：

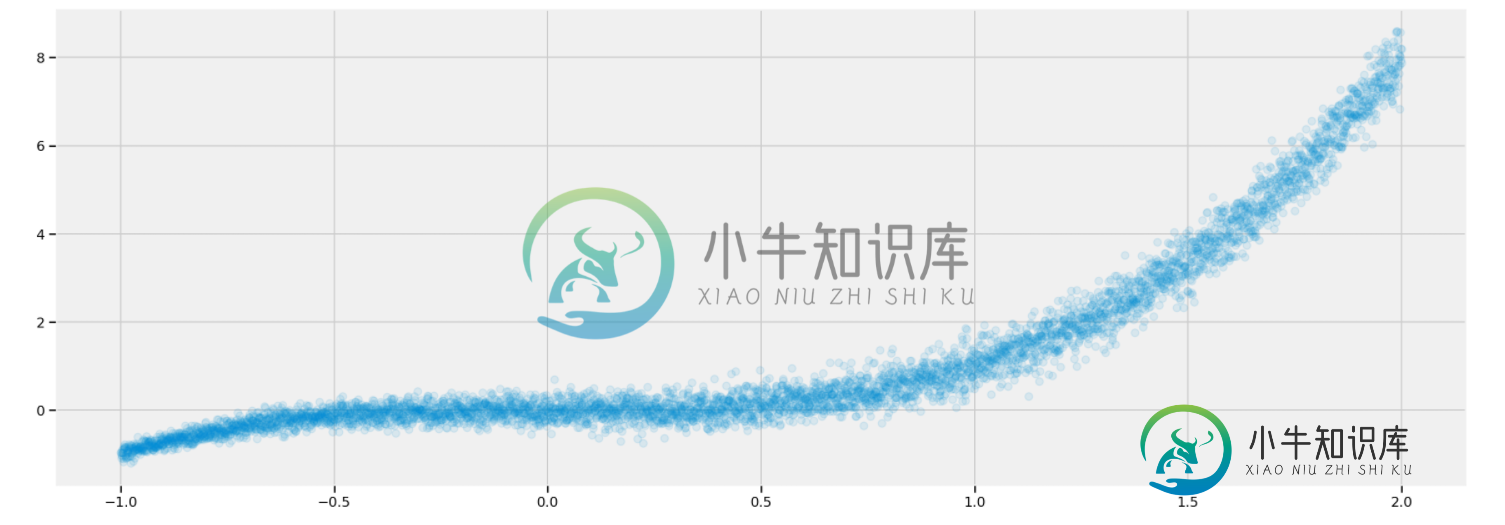
# Create and plot 5000 data points

x_train = np.linspace(-1, 2, 5000)[:, np.newaxis]
y_train = np.power(x_train, 3) + 0.1*(2+x_train)*np.random.randn(5000)[:, np.newaxis]

plt.scatter(x_train, y_train, alpha=0.1)
plt.show()

# Define the prior weight distribution -- all N(0, 1) -- and not trainable

def prior(kernel_size, bias_size, dtype = None):
    
    n = kernel_size + bias_size
    
    prior_model = Sequential([
        
        tfpl.DistributionLambda(
        
            lambda t: tfd.MultivariateNormalDiag(loc = tf.zeros(n)  ,  scale_diag = tf.ones(n)
                                                
                                                ))
        
    ])
    
    return(prior_model)

# Define variational posterior weight distribution -- multivariate Gaussian

def posterior(kernel_size, bias_size, dtype = None):
    
    n = kernel_size + bias_size
    
    posterior_model = Sequential([
        
        tfpl.VariableLayer(tfpl.MultivariateNormalTriL.params_size(n)  , dtype = dtype),   # The parameters of the model are declared Variables that are trainable
        
        tfpl.MultivariateNormalTriL(n)  # The posterior function will return to the Variational layer that will call it a MultivariateNormalTril object that will have as many dimensions
                                        # as the parameters of the Variational Dense Layer.  That means that each parameter will be generated by a distinct Normal Gaussian shifted and scaled
                                        # by a mu and sigma learned from the data, independently of all the other weights.  The output of this Variablelayer will become the input to the
                                        # MultivariateNormalTriL object.
                                        # The shape of the VariableLayer object will be defined by the number of paramaters needed to create the MultivariateNormalTriL object given
                                        # that it will live in a Space of n dimensions (event_size = n).  This number is returned by the tfpl.MultivariateNormalTriL.params_size(n)
        
        
    ])
    
    return(posterior_model)

x_in = Input(shape = (1,))

x = tfpl.DenseVariational(units= 2**4,
                          make_prior_fn=prior,
                          make_posterior_fn=posterior,
                          kl_weight=1/x_train.shape[0],
                          activation='relu')(x_in)

x = tfpl.DenseVariational(units= 2**4,
                          make_prior_fn=prior,
                          make_posterior_fn=posterior,
                          kl_weight=1/x_train.shape[0],
                          activation='relu')(x)

x =    tfpl.DenseVariational(units=tfpl.IndependentNormal.params_size(1),
                          make_prior_fn=prior,
                          make_posterior_fn=posterior,
                          kl_weight=1/x_train.shape[0])(x)

y_out =  tfpl.IndependentNormal(1)(x)

model = Model(inputs = x_in, outputs = y_out)

def nll(y_true, y_pred):
    return -y_pred.log_prob(y_true)

model.compile(loss=nll, optimizer= 'Adam')
model.summary()

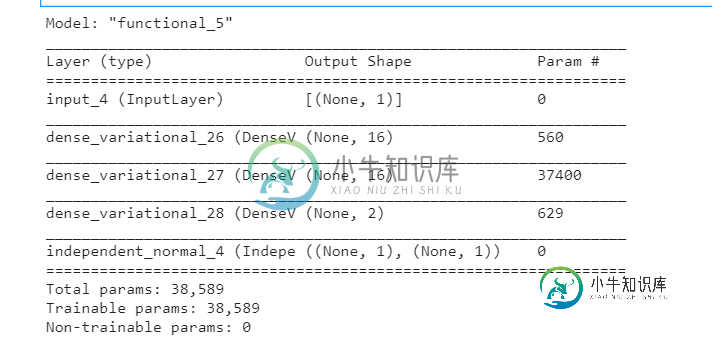
history = model.fit(x_train1, y_train1, epochs=500)

Answer 1

该模型有38，589个可训练参数，但您只有5，000个点作为数据；因此，在如此多的参数下，有效的训练是不可能的。

Answer 2

问题似乎出在损失函数中：没有任何指定位置和尺度的独立正态分布的负对数似然导致未驯服的方差，从而导致最终损失值的爆炸。由于您正在试验变分层，因此您必须对认识不确定性的估计感兴趣，为此，我建议应用常数方差。

我试图在以下几行代码中对您的代码进行一些细微的更改：

> < li>

首先，最终输出y_out直接来自最终变分层，没有任何独立正态分布层:

y_out =    tfpl.DenseVariational(units=1,
                  make_prior_fn=prior,
                  make_posterior_fn=posterior,
                  kl_weight=1/x_train.shape[0])(x)

其次，损失函数现在包含所需的正态分布的必要计算，但带有静态方差，以避免在训练期间损失放大：

 def nll(y_true, y_pred):
                   dist = tfp.distributions.Normal(loc=y_pred, scale=1.0)
                   return tf.reduce_sum(-dist.log_prob(y_true))

然后，以与之前相同的方式编译和训练模型:

 model.compile(loss=nll, optimizer= 'Adam')
 history = model.fit(x_train, y_train, epochs=3000)

最后，让我们从训练的模型中抽取 100 个不同的预测，并绘制这些值以可视化模型的认识不确定性：

 predicted = [model(x_train) for _ in range(100)]
 for i, res in enumerate(predicted):
                   plt.plot(x_train, res , alpha=0.1)
 plt.scatter(x_train, y_train, alpha=0.1)
 plt.show()

经过3000个周期后，结果如下所示(为了加快训练速度，训练点数从5000点减少到3000点):