找到一个永远完整的二叉查找树的根

Question

我需要制作一个完整的二叉搜索树。如果我有一个看起来像这样的方法：

public void createCompleteTree(Node n, int i)

例如，我用数字9作为< code>i的值，我该怎么做才能找到一个根来生成一棵完整的树呢？

如果我使用9作为值，则数字将为1，2，3，4，5，6，7，8，9。对于完整的二叉搜索树，根必须为 6，如下所示：

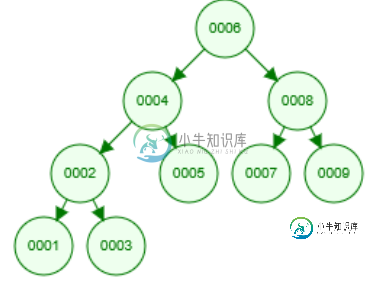
我怎样才能制作一个知道这一点的方法？它应该适用于任何类型的数字，所以如果我想使用数字14，它应该能够。

到目前为止，我唯一拥有的代码是一个插入方法，它只是检查要插入的数字是大于（向右）还是小于（向左）而不是我们目前所在的节点。x 是要插入的数字，t 是我们在树中的当前节点：

 private BinaryNode<AnyType> insert( AnyType x, BinaryNode<AnyType> t )
{
    if( t == null )
        return new BinaryNode<>( x, null, null );

    int compareResult = x.compareTo( t.element );

    if( compareResult < 0 )
        t.left = insert( x, t.left );
    else if( compareResult > 0 )
        t.right = insert( x, t.right );
    else
        ;  // Duplicate; do nothing
    return t;
}

Answer 1

二叉树的根不必是常数。存在自平衡树。看看这个:在这里输入链接描述

Answer 2

这是解决方案:

据我所知，计算偏移量是通过在长度上增加每个额外元素的偏移量，直到达到1/2的水平宽度。因此，高度为4的BST在最低层有8个元素。大小为8、9、10、… 15的列表创建高度为4的BST。对于那些列表，列表的根索引是4，5，6，7，7，7，7，7。

似乎有效

private int calcMid(int length) {
    if ( length <= 4 )
        return length / 2;
    int levelSize = 1;
    int total = 1;
    while ( total < length ) {
        levelSize *= 2;
        total += levelSize;
    }
    int excess = length - (total - levelSize);
    int minMid = (total - levelSize + 1) / 2;
    if ( excess <= levelSize / 2 ) {
        return minMid + (excess - 1); 
    } else {
        int midExcess = levelSize/2; 
        return minMid + (midExcess - 1);
   }
}

作为此代码的一部分:

https://stackoverflow.com/a/52749727/9899617

Answer 3

具有 N 个级别的二叉树可能包含从 2^（N-1） 到 2^N - 1 的元素。
您描述的最后一个（最低）级别的树可以按严格顺序包含 1 到 2^（N-1） 个元素。
具有 K 个元素和 N 个级别的树在其最后一个级别包含 K - 2^（N-1） 1 个元素。此树的左侧子树包含 C = 最小（K - 2^（N-1） 1， 2^（N-2）） 元素。所以树的根将是2^（N-2）C-th个元素