求两个三角形之间最小距离的算法

Question

在数学上问这个可能更好。是的，但我先试试这里：

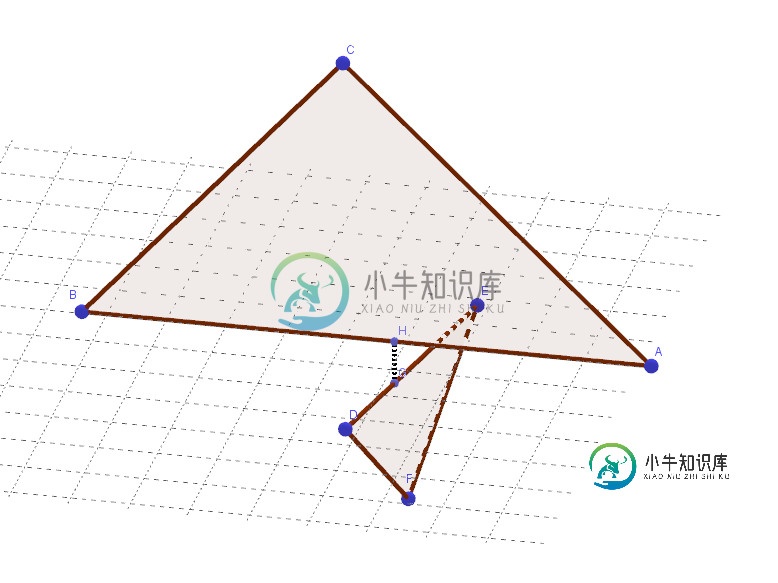
假设三角形不是共面的，我知道代表两个三角形之间最小距离的一个点必须位于其中一个三角形的顶点或沿边。对于另一个三角形，它可以位于平面上的任何位置，包括沿边或顶点。

实际上，我不需要最小距离本身——最终，我需要找到的只是三角形是否在彼此的某个epsilon内。

我尝试过的一件事是简单地对曲面进行采样，并应用快速ε测试，以查看一个三角形中的任何点是否在另一个三角形上的任何点的ε范围内，但这对我的应用程序来说太慢了。在我看来，这应该有一个直接的解析解，但我还没有找到关于这个问题的任何东西。

Answer 1

正如Axel评论中提到的，可以在PQP-Proximity Query Pack（特别是TriDist.cpp文件）中找到一个实现。然而，该算法没有附带的引用，我也找不到埃里克·拉森的任何东西，他显然是写的（事实上，这篇2014年的论文也提到，除了PQP源html" target="_blank">代码，他们找不到该算法的任何出版物）。

该算法的要点非常简单：

首先，找出每对边之间的最小距离（总共9个组合）。在这里，PQP使用以下算法：

弗拉基米尔J.线段间距离的快速计算。信息处理信件，第21号，第55-61, 1985页。

请注意，我已经将我们正在比较的两条边的顶点着色为蓝色，而离边顶点现在是绿色的。我们现在查看边缘顶点，并检查它们是否在两个平面之间的平板内。因为顶点D在两个平面之间，我们知道我们没有找到两个三角形之间的真正最小距离。

因为两个边外顶点都在两个平面之外，所以我们可以保证找到了两个三角形之间的最小距离。

在二维中，可以保证最小距离沿两个三角形的边，但在三维中并非如此。如果上述检查未找到最小距离（即，没有一对边通过平面测试），则以下情况之一必须为真：

1. 其中一个最近点是一个三角形的顶点，另一个最近点在另一个三角形的面上
2. 三角形相交
3. 一个三角形的边平行于另一个三角形的面
4. 一个或两个三角形是退化的

首先，你必须检查案例1：

将第一个三角形的点投影到第二个三角形上，并取投影点与第一个三角形法线的点积。所有的点积都应该有相同的符号（如果没有，交换你操作的三角形）。然后，找到投影最短的顶点，检查它的投影实际上位于另一个三角形的表面。如果是这样，你已经找到了你的两点（你正在看的顶点，以及它在另一个三角形上的投影）。

否则，它必须属于情况2-4。

如果这两个三角形在之前的检查中显示为不相交，则情况3或4。不管怎样，只需使用第一次测试中发现的最小点即可。否则，必须是情况2，在这种情况下，最小距离为零。