查找最小开销路径javascript

Question

给定一个成本矩阵cost[][]和cost[][]中的一个位置(m，n)，写一个函数，返回从（0,0）到(m，n)的最小成本路径的成本。矩阵的每个单元格表示遍历该单元格的成本。一条路径到达(m，n)的总成本是该路径上所有成本的总和（包括源和目的地）。您只能从给定的单元格中向下、向右和沿对角线向下遍历单元格，即从给定的单元格(i，j)，可以遍历单元格(i+1，j)，(i，j+1)和(i+1，j+1)。您可以假定所有成本都是正整数。

例如，在下图中，到（2,2）的最小成本路径是什么？

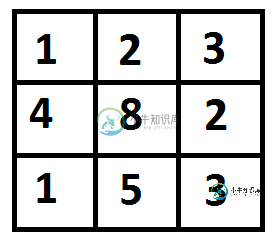
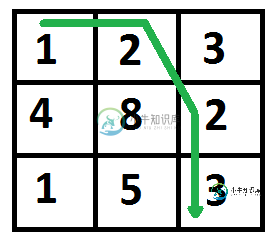
下图突出显示了成本最小的路径。路径是（0,0)->(0,1)->(1,2)->(2,2）。路径的开销为8(1+2+2+3)。

function minCost(array, m, n){

    let tc = [m+1][n+1]
    tc[0][0] == array[0][0]

    for (let i = 1; i <= m; i++) {
        tc[i][0] = tc[i-1][0] + cost[i][0]
    }

    for (i = 1; i <= m; i++){
            tc[i][0] = tc[i-1][0] + cost[i][0];
    }
 
        /* Initialize first row of tc array */
    for (j = 1; j <= n; j++){
        tc[0][j] = tc[0][j-1] + cost[0][j];
    }
 
        /* Construct rest of the tc array */
    for (i = 1; i <= m; i++){
        for (j = 1; j <= n; j++){
            tc[i][j] = min(tc[i-1][j-1],tc[i-1][j], tc[i][j-1]) + cost[i][j];
            }
    }
 
        return tc[m][n];
}
console.log(minCost([
    [1,2,3],
    [4,8,2],
    [1, 5, 3]
],2,2))

我面临一个问题来解决这个算法问题。所以我尝试了一些方法，但代码出现了错误。有人能识别出我的代码中的问题在哪里吗？

Answer 1

您的代码看起来几乎正确，除了两个问题：

• 使用成本数组，而函数参数为数组。

到处用array替换cost（但是cost名称要好得多:)，因此可以用cost)替换array)

null