C++实现二叉树遍历序列的求解方法
本文详细讲述了C++实现二叉树遍历序列的求解方法,对于数据结构与算法的学习有着很好的参考借鉴价值。具体分析如下:
一、由遍历序列构造二叉树
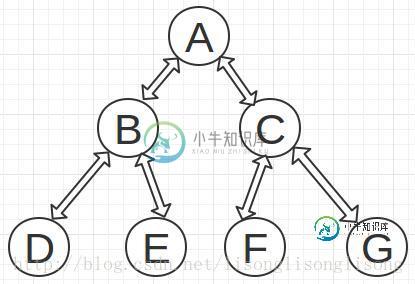
如上图所示为一个二叉树,可知它的遍历序列分别为:
先序遍历:ABDECFG
中序遍历:DBEAFCG
后序遍历:DEBFGCA
我们需要知道的是,由二叉树的先序序列和中序序列可以唯一地确定一棵二叉树;由二叉树的后序序列和中序序列也可以唯一地确定一棵二叉树;但是如果只知道先序序列和后序序列,则无法唯一确定一棵二叉树。
二、已知二叉树的先序序列和中序序列,求后序序列。
因为由二叉树的先序序列和中序序列可以唯一地确定一棵二叉树,所以进而可以唯一地确定它的后序遍历。在先序遍历序列中,第一个结点一定是二叉树的根结点,而在中序遍历中,根结点必然将中序序列分割成两个子序列,前一个子序列就是左子树的中序序列,后一个子序列就是右子树的中序序列。根据这两个子序列的长度,可以在先序序列中找到对应的左子树先序序列和右子树先序序列。而左子树先序序列的第一个结点是左子树的根结点,右子树先序序列的第一个结点是右子树的根结点。如此递归地进行下去,便能唯一地确定这棵二叉树。
C++实现代码如下:
/*************************************************************************
> File Name: Test.cpp
> Author: SongLee
************************************************************************/
#include<iostream>
using namespace std;
struct TreeNode
{
struct TreeNode* left;
struct TreeNode* right;
char elem;
};
TreeNode* PostOrderFromOrderings(char* inorder, char* preorder, int length)
{
if(length == 0)
{
return NULL;
}
TreeNode* node = new TreeNode;
node->elem = *preorder;
int rootIndex = 0;
for(; rootIndex < length; rootIndex++) // 求左子树的长度
{
if(inorder[rootIndex] == *preorder)
break;
}
node->left = PostOrderFromOrderings(inorder, preorder + 1, rootIndex);
node->right = PostOrderFromOrderings(inorder + rootIndex + 1, preorder + rootIndex + 1, length - (rootIndex + 1));
cout << node->elem << " "; // 求后序序列,所以最后输出根结点
return node;
}
int main()
{
char* pre = "ABDECFG";
char* in = "DBEAFCG";
PostOrderFromOrderings(in, pre, 7);
cout << endl;
return 0;
}
三、已知二叉树的后序序列和中序序列,求先序序列。
同理,由二叉树的后序序列和中序序列也可以唯一地确定一棵二叉树,所以进而可以唯一地确定先序遍历序列。因为后序序列的最后一个结点就如同先序序列的第一个结点,可以将中序序列分割成两个子序列,然后采用类似的方法递归地进行划分。
C++实现代码如下:
/*************************************************************************
> File Name: Test1.cpp
> Author: SongLee
************************************************************************/
#include<iostream>
using namespace std;
struct TreeNode
{
struct TreeNode* left;
struct TreeNode* right;
char elem;
};
TreeNode* PreOrderFromOrderings(char* inorder, char* postorder, int length)
{
if(length == 0)
{
return NULL;
}
TreeNode* node = new TreeNode;
node->elem = postorder[length-1];
int rootIndex = 0;
for(; rootIndex < length; rootIndex++) // 求左子树的长度
{
if(inorder[rootIndex] == postorder[length-1])
break;
}
cout << node->elem << " "; // 求先序序列,所以先输出根结点
node->left = PreOrderFromOrderings(inorder, postorder, rootIndex);
node->right = PreOrderFromOrderings(inorder + rootIndex + 1, postorder + rootIndex, length - (rootIndex + 1));
return node;
}
int main()
{
char* post = "DEBFGCA";
char* in = "DBEAFCG";
PreOrderFromOrderings(in, post, 7);
cout << endl;
return 0;
}
相信本文所述实例对于大家学习数据结构与算法会起到一定的帮助作用。
-
我正在尝试实现一个levelOrder函数,它接受树的指针并逐级打印树的数据。这是《C如何编程》一书中的一个问题,完整问题如下: (级序二叉树遍历)Fig的程序。12.19说明了遍历二叉树的三种递归方法——顺序遍历、前序遍历和后序遍历。此练习演示了二叉树的级别顺序遍历,其中节点值从根节点级别开始逐级打印。每个级别上的节点从左到右打印。级序遍历不是递归算法。它使用队列数据结构来控制节点的输出。算法如
-
本文向大家介绍通过先序遍历和中序遍历后的序列还原二叉树(实现方法),包括了通过先序遍历和中序遍历后的序列还原二叉树(实现方法)的使用技巧和注意事项,需要的朋友参考一下 当我们有一个 先序遍历序列:1,3,7,9,5,11 中序遍历序列:9,7,3,1,5,11 我们可以很轻松的用笔写出对应的二叉树。但是用代码又该如何实现? 下面我们来简单谈谈基本思想。 首先,先序遍历的顺序是根据 根-左孩子-右孩
-
为了上课,我必须创建一个状态对象的二叉树,每个状态对象包括一个居民对象的二叉树,这些居民对象组织住在每个州的人。我试图在一个给定的州中搜索最老的居民;然而,居民是按字母顺序组织在树中的,这对我的搜索毫无帮助。因此,我必须遍历整个居民树,更新保存最老的人的节点,并在树被完全遍历后返回它。我已经有了代码的第一部分,但是还停留在如何写递归的剩余部分。 状态树的方法: 然后是公共“包装器”状态树方法:
-
中序遍历二叉树 按完全二叉树的层次遍历给出一棵二叉树的遍历序列(其中用0表示虚结点),要求输出该二叉树的深度及中序遍历该二叉树得到的序列。 输入格式: 首先输入一个整数T,表示测试数据的组数,然后是T组测试数据。每组测试数据首先输入一个正整数n(n≤1000),代表给出的二叉树的结点总数(当然,其中可能包含虚结点)。结点编号均为正整数,且各不相同。 然后输入n个正整数,表示按完全二叉树(即第1层1
-
本文向大家介绍C#使用前序遍历、中序遍历和后序遍历打印二叉树的方法,包括了C#使用前序遍历、中序遍历和后序遍历打印二叉树的方法的使用技巧和注意事项,需要的朋友参考一下 本文实例讲述了C#使用前序遍历、中序遍历和后序遍历打印二叉树的方法。分享给大家供大家参考。具体实现方法如下: 希望本文所述对大家的C#程序设计有所帮助。
-
本文向大家介绍C++实现二叉树非递归遍历方法实例总结,包括了C++实现二叉树非递归遍历方法实例总结的使用技巧和注意事项,需要的朋友参考一下 一般来说,二叉树的遍历是C++程序员在面试中经常考察的,其实前中后三种顺序的遍历都大同小异,自己模拟两个栈用笔画画是不难写出代码的。现举一个非递归遍历的方法如下,供大家参考。 具体代码如下: 希望本文所述对大家的C++算法学习有所帮助。

