Opencv实现傅里叶变换

傅里叶变换将图像分解成其正弦和余弦分量，它将图像由空域转换为时域。任何函数都可以近似的表示为无数正弦和余弦函数的和，傅里叶变换就是实现这一步的，数学上一个二维图像的傅里叶变换为：

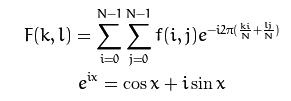
公式中，f是图像在空域的值，F是频域的值。转换的结果是复数，但是不可能通过一个真实图像和一个复杂的图像或通过大小和相位图像去显示这样的一个图像。然而，在整个图像处理算法只对大小图像是感兴趣的，因为这包含了所有我们需要的图像几何结构的信息。

可通过以下几步显示一副傅里叶变换后的图像

1、将图像扩展到它的最佳尺寸，DFT(直接傅里叶变换)的性能依赖于图片的尺寸，当图像是2，3，5的倍数时往往是最快的。因此，为了达到最优性能通常采用垫边界值的方法，得到一个最佳的尺寸。

2、为傅立叶变换结果的实部和虚部分配存储空间。傅里叶变换的结果是一个复数，这意味着每幅图的结果都有一个实部和虚部，此外，频域范围远远大于它对应的空间范围。因此，我们这些通常至少以一个浮点数格式存储这些数值。因此，我们会将我们的输入图像转换为这种类型并且扩展它与另一通道存放复数值

3、进行傅里叶变换。

4、将复数转换为幅值，DFT的幅值由以下公式得出：

5、切换到对数刻度。对图像进行对数尺度的缩放，结果证明，傅立叶系数矩阵的动态范围太大，无法显示在屏幕上，我们无法通过这样去观察一些小的和高的变化值。因此那些高的数值将转化成白点而小的数值会变成黑点，使用灰度值进行可视化，我们可以将线性刻度转换为对数刻度，以便于观察。

6、剪切和重分布幅度图象，第一步我们扩展了图像，这里我们去掉扩展的那部分值，基于可视化的目的，我们还可以重新排列结果的象限，使原点(0，0)对应于与图像中心

7、归一化。目前得到的幅值图像仍然太大，超出了显示的范围，归一化这范围内的值，可以进一步达到可视化的目的

实现程序

void _DFT(){
 //1以灰度模式读取原图像并显示
 Mat srcImage = imread("miFan.jpg",0);
 if (!srcImage.data){ cout << "Error\n"; }
 imshow("原图像", srcImage);

 //2将输入图像扩展到最佳尺寸,边界用0补充
 int m = getOptimalDFTSize(srcImage.rows);
 int n = getOptimalDFTSize(srcImage.cols);

 //将添加的像素初始化为0
 Mat padded;
 copyMakeBorder(srcImage, padded, 0, m - srcImage.rows,
  0, n - srcImage.cols, BORDER_CONSTANT, Scalar::all(0));

 //3为傅里叶变换的结果(实部和虚部)分配存储空间
 //将数组组合合并为一个多通道数组
 Mat planes[] = { Mat_<float>(padded), Mat::zeros(padded.size(), CV_32F) };
 Mat complexI;
 merge(planes, 2, complexI);

 //4进行傅里叶变换
 dft(complexI, complexI);

 //5将复数转换为幅值，即=> log(1 + sqrt(Re(DFT(I))^2 + Im(DFT(I))^2))
 //将多通道数组分离为几个单通道数组
 split(complexI, planes);//planes[0] = Re(DFT(I), planes[1] = Im(DFT(I))
 magnitude(planes[0], planes[1], planes[0]);
 Mat magImage = planes[0];

 //6进行对数尺度缩放
 magImage += Scalar::all(1);
 log(magImage, magImage);//求自然对数

 //7剪切和重分布幅度图象限
 //若有奇数行或奇数列，进行频谱剪裁
 magImage = magImage(Rect(0, 0, magImage.cols&-2, magImage.rows&-2));
 //重新排列傅立叶图像中的象限，使得原点位于图像中心 
 int cx = magImage.cols / 2;
 int cy = magImage.rows / 2;
 Mat q0(magImage, Rect(0, 0, cx, cy));
 Mat q1(magImage, Rect(cx, 0, cx, cy));
 Mat q2(magImage, Rect(0,cy,cx,cy));
 Mat q3(magImage, Rect(cx,cy,cx,cy));
 //交换象限(左上与右下进行交换)
 Mat tmp;
 q0.copyTo(tmp);
 q3.copyTo(q0);
 tmp.copyTo(q3);
 //交换象限（右上与左下进行交换）
 q1.copyTo(tmp);
 q2.copyTo(q1);
 tmp.copyTo(q2);

 //8归一化，用0到1的浮点值将矩阵变换为可视的图像格式
 normalize(magImage, magImage, 0, 1, CV_MINMAX);

 //9显示
 imshow("频谱增幅", magImage);

 waitKey();
}

傅里叶变换后的图片

以上就是本文的全部内容，希望对大家的学习有所帮助，也希望大家多多支持小牛知识库。